Рассмотрим пример.
Вычислить приближенное значение определенного интеграла 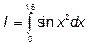 с помощью формулы Симпсона, положив n=4.
с помощью формулы Симпсона, положив n=4.
Формула Симпсона приближенного интегрирования позволяет численно определить значение интеграла без нахождения первообразной. Для этого достаточно вычислить значение функции в n=4 точках, полученных в результате разбиения отрезка 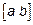 на n отрезков (n – четное число)
на n отрезков (n – четное число) 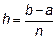 шаг разбиения
шаг разбиения 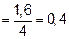
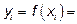 значение подынтегральной функции на концах отрезков.
значение подынтегральной функции на концах отрезков.
Составим таблицу:
| K | 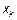
| 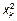
| 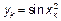
|
| 0,00 | 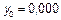
| ||
| 0,4 | 0,16 | 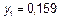
| |
| 0,8 | 0,64 | 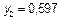
| |
| 1,2 | 1,44 | 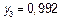
| |
| 1,6 | 2,56 | 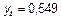
|
Формула Симпсона
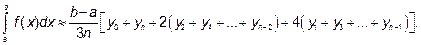
Подставив в эту формулу конкретные значения, получим
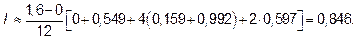
Вычислять интегралы приближённо можно не только при помощи метода Симпсона, но и других методов. Подробнее об этих методах можно прочитать в[1] гл. XIII ,[4] гл.11 пр.8
Решите самостоятельно задачу:
18.1 Найдите число 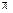 , пользуясь интегралом
, пользуясь интегралом 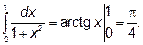
Дата добавления: 2014-12-09; просмотров: 654;
