ЗАДАНИЕ №21
Следующая задача об экстремумах функций двух переменных и об отыскании наибольших и наименьших значений функции двух независимых переменных. Функция ограниченная и дифференцируемая в замкнутой области достигает в этой области своего наибольшего и наименьшего значения или во внутренних точках этой области, которые являются точками стационарности функции или на её границе. Для того, чтобы найти наибольшее и наименьшее значение функции, надо:
1) Найти стационарные точки функции, для чего следует решить систему уравнений 
2) Вычислить в стационарных точках значения функции
3) Найти наибольшие и наименьшее значение функции на каждой линии, ограничивающей область;
4) Сравнить все полученные значения. Наибольшее из них будет наибольшим, а наименьшее – наименьшим значением функции в замкнутой области.
Пример 1.Найти наибольшее и наименьшее значение функции 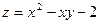 в ограниченной замкнутой области D:
в ограниченной замкнутой области D: 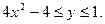
Решение: Точка  являются точкой экстремума (максимума или минимума) функции z=f(x,y), если значение функции в этой точке соответственно больше или меньше значений, принимаемых ее в некоторой окрестности точки
являются точкой экстремума (максимума или минимума) функции z=f(x,y), если значение функции в этой точке соответственно больше или меньше значений, принимаемых ее в некоторой окрестности точки 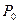 , то есть при всех x и y достаточно близких к
, то есть при всех x и y достаточно близких к 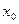 и
и 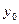 . Точка P, координаты которой обращают в нуль обе частные производные функции f(x,y) называются стационарной точкой этой функции.
. Точка P, координаты которой обращают в нуль обе частные производные функции f(x,y) называются стационарной точкой этой функции.
- Найдем стационарные точки функции z(x,y)

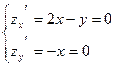
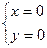
Стационарная точка y функции z одна. Это точка 0.
- Входит ли точка (0,0) в область D? Построим эту область.
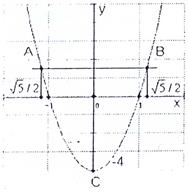
- 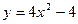 - парабола с вершиной в точке (0,-4). Точки пересечения с осью x:
- парабола с вершиной в точке (0,-4). Точки пересечения с осью x: 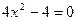 ,
, 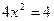 ,
, 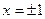
- y=0 – ось x.
Точка (0,0) входит в область D. Установим, является ли стационарная точка 0 точкой экстремума. Это делается так: Пусть 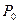 стационарная точка функции z=f(x,y). Вычислим в этой точке
стационарная точка функции z=f(x,y). Вычислим в этой точке
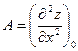 .
.  .
. 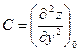
Если 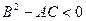 , то функция f(x,y) имеет в точке
, то функция f(x,y) имеет в точке 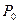 экстремум:
экстремум:
max-при A<0 и min при A>0.
Если 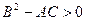 , то точка
, то точка 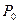 не является точкой экстремума.
не является точкой экстремума.
Если 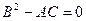 , то требуется дополнительное исследование.
, то требуется дополнительное исследование.
Исследуем нашу функцию z по формулам.
3. 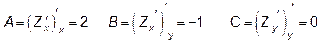
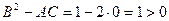 , точка (0,0) не является точкой экстремума.
, точка (0,0) не является точкой экстремума.
4. Исследуем поведение функции на границе.
Так как Z не имеет ни max ни min, ее наибольшим и наименьшем значением является наибольшее и наименьшее из значений, принимаемых на границе.
Для того, чтобы найти наибольшее или наименьшее из значений, принимаемых на границе.
4а. Рассмотрим верхнюю границу y=1. На ней функция Z(x,1) превращается в 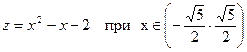
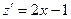 ,
, 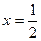 в этой точке возможен экстремум. Знак производной меняется с – на +, то есть в точке
в этой точке возможен экстремум. Знак производной меняется с – на +, то есть в точке 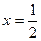 - минимум z =-2.25
- минимум z =-2.25
при 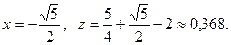
В точке 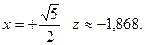
4б. Рассмотрим нижнюю границу 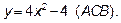
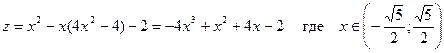
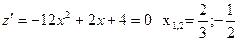
В точке 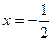 производная меняет знак с - на +, следовательно, это точка минимума
производная меняет знак с - на +, следовательно, это точка минимума 

В точке 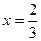 производная меняет знак с + на -, следовательно, это точка максимума
производная меняет знак с + на -, следовательно, это точка максимума  . При
. При 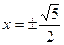 функция z уже вычислялось. Видим, что от
функция z уже вычислялось. Видим, что от 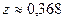 функция убывает до
функция убывает до 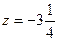 , затем возрастает до
, затем возрастает до 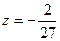 а затем убывает до
а затем убывает до 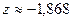 .
.
То есть наименьшее значение для всей границы 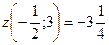 , а наибольшее
, а наибольшее 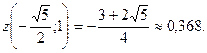
Ответ: Наибольшее значение функции z в замкнутой области D 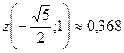 , наименьшее
, наименьшее 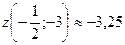 .
.
Подробнее об этом можно почитать в [1] гл.XV, [4] гл.8, и найти аналогичные задачи в [3] гл.8
Решите самостоятельно следующие задачи:
21.1 Найдите наибольшее и наименьшие значение функции 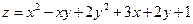 в замкнутом треугольнике, ограниченном осями координат и прямой x+y+5=0
в замкнутом треугольнике, ограниченном осями координат и прямой x+y+5=0
21.2 Найти наибольшее и наименьшее значения функции z=xy(x+y+1) в замкнутой области, ограниченной линиями 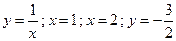
21.3 Доказать, что из всех треугольников, имеющих данный периметр 2p наибольшую площадь имеет равносторонний треугольник.
Дата добавления: 2014-12-09; просмотров: 1092;
