ЗАДАНИЕ №24
Следующая задача относится к вычислению тройного интеграла
Тройным интегралом от функции  по области Ư называется предел интегральной суммы при условии, что
по области Ư называется предел интегральной суммы при условии, что
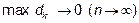 , где d- диаметр частичной области разбиения
, где d- диаметр частичной области разбиения

Для непрерывной в области U функции этот предел существует и не зависит от способа разбиения области U на элементарные и от выбора точек Рк (теорема о существовании тройного интеграла).
Если 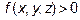 в области U, то тройной интеграл
в области U, то тройной интеграл 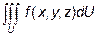 физически есть масса тела, занимающего область U и имеющего переменную плотность
физически есть масса тела, занимающего область U и имеющего переменную плотность 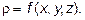
В частности, если 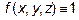 , то тройной интеграл определяет объем области U,т.е.
, то тройной интеграл определяет объем области U,т.е.
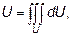
dU – элемент объёма.
Основные свойства тройных интегралов аналогичны свойствам двойных интегралов.
В декартовых координатах тройной интеграл обычно записывают в виде:
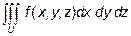
Вычисление тройного интеграла
Пусть область интегрирования U определяется неравенствами:
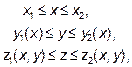
Где y1(x), y2(x), z1( x, y), z2(x, y) – непрерывные функции. Тогда тройной интеграл от функции  по области U вычисляется по формуле:
по области U вычисляется по формуле:
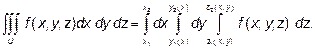
Интеграл стоящий в правой части формулы называется трехкратным. Он принципиально мало чем отличается от двукратного, добавляется лишь интегрирование еще по одной переменной.
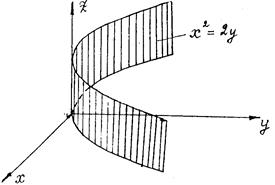
Пример 1.Вычислить с помощью тройного интеграла объём тела, ограниченного
поверхностями
z=0, z=4-y2, x2=2y.
 Решение: Данное тело ограничено сверху цилиндрической поверхностью z=4-y2 с образующими, параллельными оси ОХ, снизу плоскостью z=0 ( координатная плоскость ХОУ ).
Решение: Данное тело ограничено сверху цилиндрической поверхностью z=4-y2 с образующими, параллельными оси ОХ, снизу плоскостью z=0 ( координатная плоскость ХОУ ).
Эти поверхности
пересекаются по
прямым:
у = -2 и у = +2
Тело U ограничено также цилиндрической поверхностью x2=2y с образующими, параллельными оси OZ
Поверхности, пересекаясь, образуют замкнутое тело, которое проецируется в область Д
плоскости ХОУ
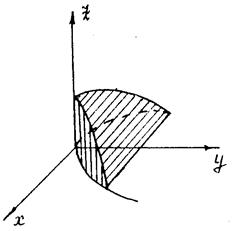
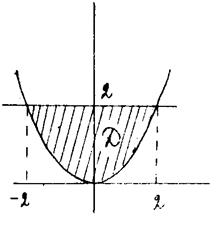
Для вычисления объёма воспользуемся формулами. Пределы интегрирования по Х и У расставятся в соответствии с областью Д (как в двухкратном интеграле), а пределами интегрирования по Z будут:
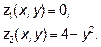

Получим
Ответ: 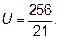
ОТВЕТЫ И УКАЗАНИЯ
1.1Перенести свободный член направо и разделить обе части уравнения на него
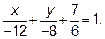
1.2Использовать направляющий вектор прямой в качестве нормального вектора плоскости x-3y+4z+9=0
2.1 Воспользуйтесь уравнением с угловым коэффициентом. Прямые перпендикулярны.
2.2 Найдите координаты точки пересечения Aданных сторон; зная координаты точек AиN, найдите координаты противоположной вершины параллелограмма по формуле определения координат середины отрезка; через найденную точку C проведите прямую, параллельную AD, а потом прямую, параллельную AB.
(BC) 2x+y-5=0
(CD) x+2y-11=0
3.1 Соберите члены уравнения, содержащие одну и ту же переменную величину в скобки. В каждой скобке выделите полный квадрат.
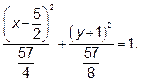 Эллипс с полуосями
Эллипс с полуосями 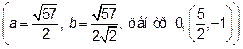
3.2 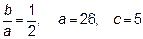 Для гиперболы
Для гиперболы 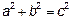 ; найти aиb,подставить в уравнение
; найти aиb,подставить в уравнение 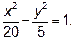
4.1 
5.1 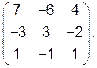
6.1 Ранг матрицы системы не равен рангу расширенной матрицы системы 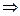 система несовместима
система несовместима
7.1 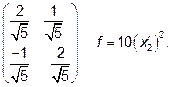
9.1. 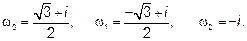
9.2 
10.1 Произведите вычитание дробей. Ответ: 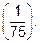
10.2 Домножьте на иррационально сопряженное выражение 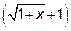 . Ответ:
. Ответ: 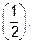
10.3 Приобразуйте выражение через sin xи cos x Ответ: (0).
10.4 Учтите, что 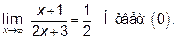
11.1 Найдите левосторонний и правосторонний пределы. Точка x=1точка разрыва первого рода.
11.2 Разрыв устранимый.
12.1 Сложная функция 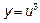
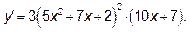
12.2 Сложная функция 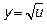
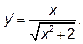
12.3 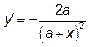 (производная дроби).
(производная дроби).
12.4 Воспользуйтесь логарифмом дроби 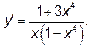
12.5 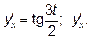
----------------------------------------------------------------------------------------
13.1 Неопределенность вида 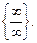
Применив 1 раз правило Лопиталя, получим неопределенность вида 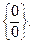 Преобразуем дробь и применим правило Лопиталя ещё раз. Получим ответ
Преобразуем дробь и применим правило Лопиталя ещё раз. Получим ответ 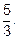
13.2 Неопределённость вида 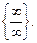
Два раза применим правило Лопиталя. Ответ: 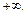
13.3 Неопределённость вида 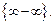
Преобразуем 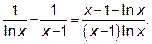
Получим неопределённость вида 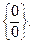 Применяем правило Лопиталя, преобразуем результат в единую дробь и ещё раз применяем правило Лопиталя. Ответ:
Применяем правило Лопиталя, преобразуем результат в единую дробь и ещё раз применяем правило Лопиталя. Ответ: 
14.1 Функция возрастает в двух бесконечных интервалах 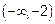 и
и  функция убывет на
функция убывет на  .
.
14.2 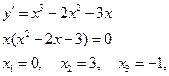
т.к. производная конечна всюду, критическими точками являются только 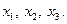 . Рассмотрим интервалы
. Рассмотрим интервалы 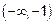 ,
,  ,
, 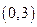 ,
, 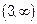 . Выберем внутри каждого из этих интервалов произвольную точку и определим в этой точке знак первой производной. Первая производная имеет в этих интервалах такую последовательность знаков:
. Выберем внутри каждого из этих интервалов произвольную точку и определим в этой точке знак первой производной. Первая производная имеет в этих интервалах такую последовательность знаков: 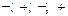 .
.
При  минимум
минимум 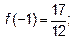
при 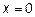 максимум
максимум 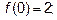
при  минимум
минимум 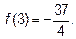
Отрезок 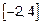 содержит внутри себя все критические точки. Так как значения в критических точках мы уже вычислили осталось вычислить значения на концах отрезка
содержит внутри себя все критические точки. Так как значения в критических точках мы уже вычислили осталось вычислить значения на концах отрезка 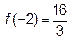 ,
, 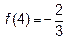 . Сравнив, видим, что наибольшим является
. Сравнив, видим, что наибольшим является 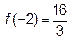 , а наименьшим
, а наименьшим 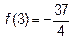 .
.
______________________________________________
14.3 Для определения горизонтальных асимптот находим 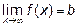 ,
, 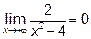 и
и 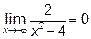 . Значит, горизонтальная асимптота одна
. Значит, горизонтальная асимптота одна  (ось
(ось 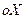 ).
).
Для определения вертикальных асимптот находим те значения  , вблизи которых
, вблизи которых 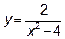 неограниченно возрастает по абсолютной величине:
неограниченно возрастает по абсолютной величине: 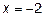 ,
, 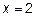 . Это и есть вертикальные асимптоты.
. Это и есть вертикальные асимптоты.
14.4 Т.к. 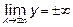 , то горизонтальных асимптот нет, т.к.
, то горизонтальных асимптот нет, т.к. 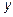 неограниченно возрастает, когда
неограниченно возрастает, когда 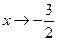
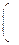
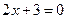 при
при  .
.
Таким образом имеется вертикальная асимптота, ее уравнение 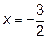 .
.
При этом 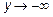 при
при 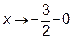 и
и 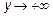 при
при 
Определим наклонные асимптоты 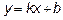 , где
, где 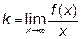 ,
, 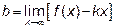

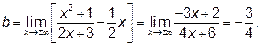
Итак, уравнение наклонной асимптоты 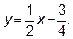
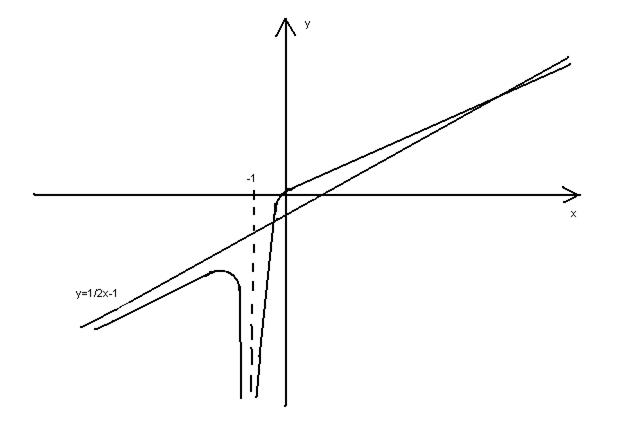
14.5. Область определения: вся числовая ось, кроме 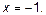 . Функция непрерывна всюду, кроме
. Функция непрерывна всюду, кроме 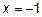 , следовательно имеется вертикальная асимптота:
, следовательно имеется вертикальная асимптота: 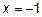 . Горизонтальных асимтот нет:
. Горизонтальных асимтот нет: 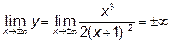 .
.
Наклонные асимптоты: 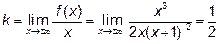 ,
, 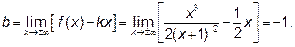
Значит, наклонная асимптота одна:
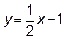
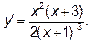
Критические точки: 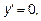 ,
, 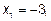 ,
, 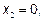 ,
, 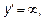 ,
, 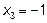 (не входит в область определения)
(не входит в область определения)
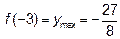
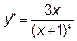


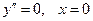

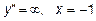 (Не рассматривается, т.к. не входит в область определения) На интервалах
(Не рассматривается, т.к. не входит в область определения) На интервалах 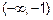 и
и 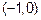 выпуклость вверх
выпуклость вверх 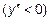 . На интервале
. На интервале 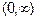 выпуклость вниз
выпуклость вниз 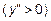 т.
т. 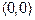 - точка перегиба.
- точка перегиба.
_________________________________________________________
15.1. Примените формулу интегрирование суммы, вынесения числового множителя за знак интеграла и интегрирование степенной функции.
Ответ: 
15.2 Замена переменных 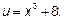 ;
; 
Подинтегральное выражение

Ответ: 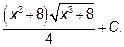
15.3 Ответ: 
15.4 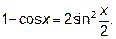
Надо применить формулу:
Ответ: 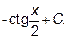
15.5 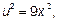
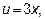
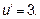
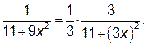
Применим формулу из таблицы с учётом, что 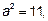
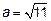
Ответ: 
16.1 Сделайте подстановку  Определите новые пределы интегрирования
Определите новые пределы интегрирования


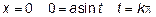


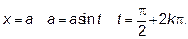
При изменении 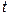 от 0 до
от 0 до 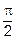 функция
функция 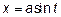 монотонно возрастает и её значения заполняют первоначальный отрезок интегрирования
монотонно возрастает и её значения заполняют первоначальный отрезок интегрирования 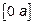
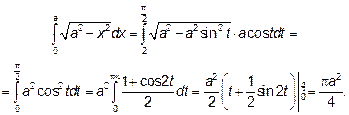
16.2 Учтите, что значение функции 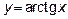 находятся на интервале
находятся на интервале
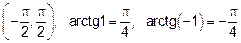
Ответ: 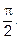
16.3 Ответ: 
16.4 Подынтегральную функцию представьте в виде 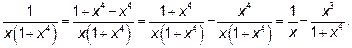 . Далее легко интегрируется.
. Далее легко интегрируется.
Ответ: 
16.5 
Применена формула интегрирования по частям.
17.1 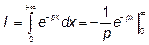 .
.
При 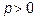 предел существует и равен
предел существует и равен 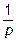 ;
;
при  интеграл расходится .
интеграл расходится .
17.2 Задача сводится к 17.1 подстановкой 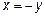 . Ответ: интеграл сходится при
. Ответ: интеграл сходится при 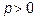 и расходится
и расходится 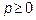 .
.
17.3 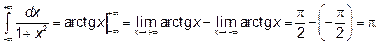
17.4 Замена переменных 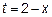 . Особенность в точке
. Особенность в точке 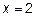 . Ответ:
. Ответ: 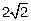
17.5 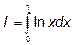 имеет особенность в точке
имеет особенность в точке 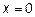
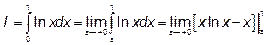
(проинтегрировали по частям)
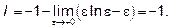
Но  (по правилу Лопиталя)
(по правилу Лопиталя)
Ответ: 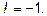
18.1 Разделите отрезок интегрирования на 10 равных частей точками

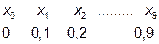
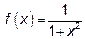


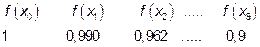
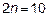 ; значит
; значит 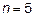

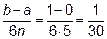
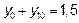

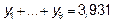
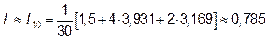
Итак, 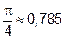 , значит
, значит  .
.
Взяв значения функций в точках деления до третьего знака, получим точность числа 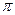 до второго знака.
до второго знака.
19.1 u - функция двух переменных х и y. Находим 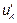 , рассматривая
, рассматривая 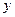 как постоянную:
как постоянную: 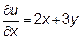 , так как производная по
, так как производная по 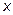 от
от 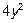 равна нулю, как производная константы
равна нулю, как производная константы 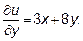
19.2 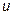 - функция трёх независимых переменных
- функция трёх независимых переменных 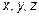 . При определении частной производной по каждой из этих переменных, две другие следует считать величинами постоянными.
. При определении частной производной по каждой из этих переменных, две другие следует считать величинами постоянными.
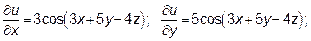
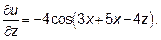
19.3 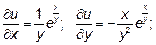 , так как
, так как 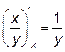 , а
, а 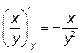 .
.
19.4 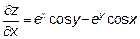
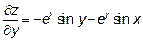
19.5 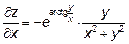
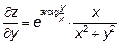
Эти производные вычислены по правилу производных сложной функции; внешняя функция-экспонента, затем 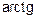 , а затем дробь
, а затем дробь 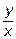 .
.
20.1.
= 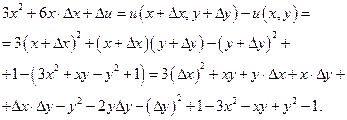 .
.
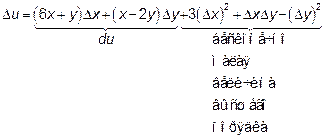
20.2 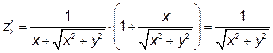
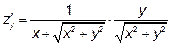
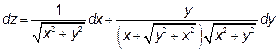
21.1 Стационарные точки:
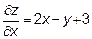
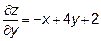
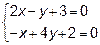 x=-2, y=-1 ,следовательно, есть одна стационарная точка (-2, -1)
x=-2, y=-1 ,следовательно, есть одна стационарная точка (-2, -1)
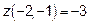
Исследуем функцию на границе области. Граница состоит из отрезка оси  , отрезка оси
, отрезка оси 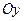 и отрезка АВ прямой
и отрезка АВ прямой
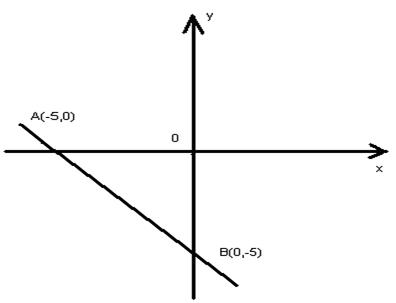
а) На оси 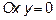 , значит
, значит 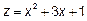 . Эта функция должна быть рассмотрена на отрезке
. Эта функция должна быть рассмотрена на отрезке 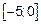 . Так как функция на отрезке непрерывна, она достигает наибольшего и наименьшего значения. Это происходит или в точках стационарности, или на концах отрезка. Определим точку стационарности
. Так как функция на отрезке непрерывна, она достигает наибольшего и наименьшего значения. Это происходит или в точках стационарности, или на концах отрезка. Определим точку стационарности 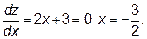 .
.
Определим значение функции при 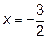 и на концах отрезка [-5,0]
и на концах отрезка [-5,0]
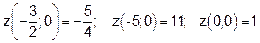
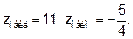
б) На оси 
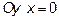 значит
значит 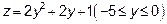
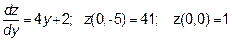

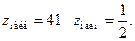
в) Исследуем функцию z на отрезке AB. Уравнение АВ 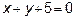 , значит
, значит 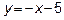
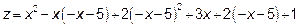
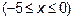
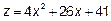

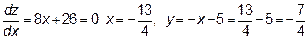
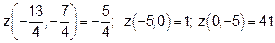

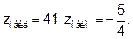
Сравним теперь значение z в стационарной точке (-2,-1) с наибольшими и наименьшими значениями на отрезках ОА, ОВ и АВ.

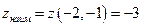 , получаем, что наименьшего своего значения функция достигла в стационарной точке
, получаем, что наименьшего своего значения функция достигла в стационарной точке 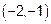 , а наибольшего – на границе области в точке (0,-5).
, а наибольшего – на границе области в точке (0,-5).
21.2 Стационарные точки 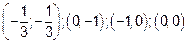 находятся вне рассматриваемой области. Наибольшего значения функция достигает на границе области в точке
находятся вне рассматриваемой области. Наибольшего значения функция достигает на границе области в точке 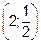 , а
, а 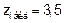 . Наименьшего значения функция достигает в точке
. Наименьшего значения функция достигает в точке 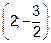 , а
, а 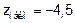 .
.
21.3 Обозначим стороны треугольника 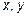 и
и 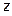 . По формуле Герона площадь треугольника
. По формуле Герона площадь треугольника 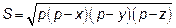 , так как
, так как  - полупериметр, то
- полупериметр, то 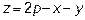 и
и 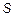 становится функцией не трёх, а только двух переменных
становится функцией не трёх, а только двух переменных
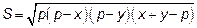
Вместо того, чтобы искать экстремум этой функции будем искать экстремум её квадрата 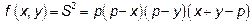 . Находим стационарные точки
. Находим стационарные точки 
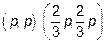
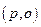
 . Исследованию подлежит только одна точка
. Исследованию подлежит только одна точка 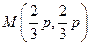 , так как остальные точки не удовлетворяют смыслу задачи(не может быть треугольника, у которого сторона равна половине периметра).
, так как остальные точки не удовлетворяют смыслу задачи(не может быть треугольника, у которого сторона равна половине периметра).
Проверяем точку М. В ней функция достигает максимума. Итак, при 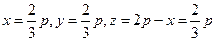
Так как 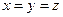 , то треугольник равносторонний.
, то треугольник равносторонний.
22.1 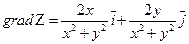
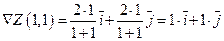
22.2 Градиент функции Z и производная по направлению a 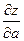 связаны формулой
связаны формулой 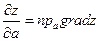 - то есть производная по направлению равна проекции вектора-градиента на вектора.
- то есть производная по направлению равна проекции вектора-градиента на вектора.
В нашем случае 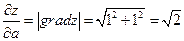
23.1 Для решения нужно представить себе область интегрирования. Решив систему
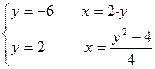
можно построить область интегрирования и найти точки пересечения линий, ограничивающих область пересечения.
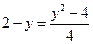
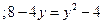
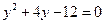
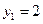

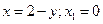
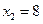
Точки пересечения 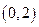 и
и 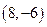 . Постройте область интегрирования. Теперь изменим порядок интегрирования, то есть внешний интеграл будем брать по
. Постройте область интегрирования. Теперь изменим порядок интегрирования, то есть внешний интеграл будем брать по  , а внутренний по
, а внутренний по 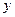 . Заметим, что в пределах изменения
. Заметим, что в пределах изменения  от -1 до 8 область интегрирования ограничена снизу одной линией: параболой, а сверху – двумя: параболой и прямой. Разобьем область интегрирования Д на две
от -1 до 8 область интегрирования ограничена снизу одной линией: параболой, а сверху – двумя: параболой и прямой. Разобьем область интегрирования Д на две 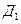 и
и 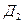 . Значит, придётся разбить наш интеграл на два. Область
. Значит, придётся разбить наш интеграл на два. Область 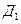 ограничена сверху и снизу ветвями параболы
ограничена сверху и снизу ветвями параболы 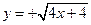 и
и 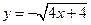 , а область
, а область 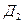 снизу ограничена ветвью параболы
снизу ограничена ветвью параболы 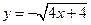 , а сверху прямой
, а сверху прямой 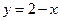 (при
(при  ).
).
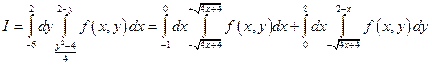
23.2 По данному уравнению построим кривую в декартовой системе координат. Из уравнения видно, что кривая симметрична и относительно 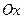 и относительно
и относительно 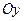 . Биссектрисы координатных углов
. Биссектрисы координатных углов 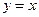 и
и 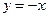 также являются осями симметрии кривой. Найдём точки пересечения с осями. При
также являются осями симметрии кривой. Найдём точки пересечения с осями. При 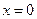
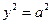 ,
, 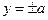 получим две точки пересечения с осью
получим две точки пересечения с осью 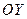
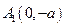 и
и 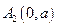 .
.
Аналогично при 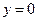 получим
получим 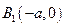 ,
, 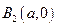 . Добавим точки при
. Добавим точки при 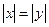
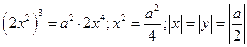
Построим кривую

Найдём площадь области Д. Перейдём в систему координат, поместив полярную ось вдоль оси 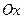 , а полюс в начало координат.
, а полюс в начало координат.
При решении геометрических и физических задач во многих случаях для упрощения вычислений двойной интеграл в прямоугольных координатах преобразуется к полярным координатам. Преобразование двойного интеграла от прямоугольных координат x, y к полярным координатам ρ, φ, связанным с прямоугольными координатами соотношениями
x= ρcosφ, y= ρsinφ, осуществляется по формуле
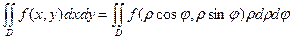
Если область интегрирования D ограничена двумя лучами, выходящими из полюса,
φ =α, φ =β (α<β) и двумя кривыми ρ= ρ1(φ) и ρ= ρ2(φ), где ρ1(φ)≤ρ2(φ), то что двойно интеграл вычисляется по формуле
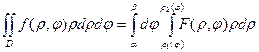 , где F(ρ, φ)=f(ρcos φ ,ρsin φ), причем сначала вычисляется интеграл
, где F(ρ, φ)=f(ρcos φ ,ρsin φ), причем сначала вычисляется интеграл 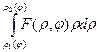 , в котором φ считается постоянным.
, в котором φ считается постоянным.

Преобразуем уравнение кривой к полярным координатам, заменив x= ρcosφ, y= ρsinφ.
Получим
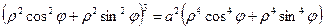
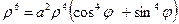
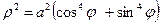 - уравнение линии в полярных координатах.
- уравнение линии в полярных координатах.
В силу симметричности кривой, площадь выразиться так:
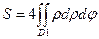
По формуле интегрирования запишем двукратный интеграл, при этом пределы интегрирования по φ будут от 0 до 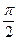 , а пределы интегрирования по ρ:
, а пределы интегрирования по ρ:
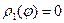
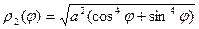
Итак
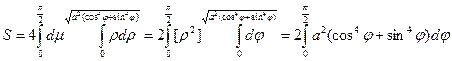 =
=
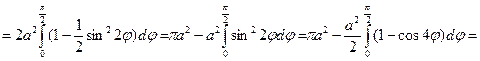
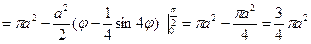 .
.
Дата добавления: 2014-12-09; просмотров: 930;
