ЗАДАНИЕ №20
Продолжим рассмотрение функции нескольких переменных. Полное приращение функции определяется по формуле: 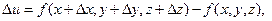 где
где 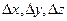 - приращения независимых переменных. По определению приращения независимых переменных
- приращения независимых переменных. По определению приращения независимых переменных 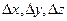 и их дифференциалы dx, dy, dz – числа равные между собой.
и их дифференциалы dx, dy, dz – числа равные между собой.
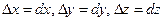 . Полный дифференциал функции
. Полный дифференциал функции 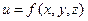
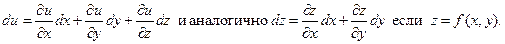 (То есть в случае функции двух переменных).Полный дифференциал функции есть главная часть её приращения, линейная относительно
(То есть в случае функции двух переменных).Полный дифференциал функции есть главная часть её приращения, линейная относительно 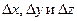 , то есть
, то есть 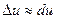 или же
или же 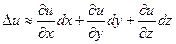 для функции трёх переменных или
для функции трёх переменных или 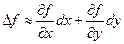 для функции двух переменных. Подробнее
для функции двух переменных. Подробнее 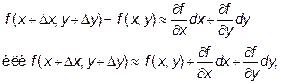 (*)
(*)
где 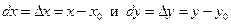 .
.
Подробнее о дифференциале функции нескольких переменных можно прочесть в [4] гл.8 или в [1] гл.15
Пример 1.Даны функции 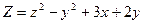 и точка М(1,02;2,05). С помощью полного дифференциала вычислить приближенное значение функции в точке М и оценить относительную погрешность.
и точка М(1,02;2,05). С помощью полного дифференциала вычислить приближенное значение функции в точке М и оценить относительную погрешность.
Решение: Приближенное значение некоторой функции f(x,y) в точке (x,y) с помощью полного дифференциала находится по формуле (*)
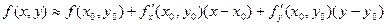 ,
,
где 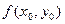 , значение функции f(x,y) в точке
, значение функции f(x,y) в точке 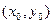 .
.
Точка 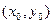 подбирается таким образом, чтобы
подбирается таким образом, чтобы 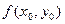 легко вычислялось;
легко вычислялось; 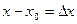 ,
, 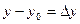 приращение функции f(x,y) в точке
приращение функции f(x,y) в точке 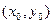 по переменным x и y соответственно.
по переменным x и y соответственно.
В качестве точки 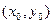 возьмем точку N(1,2), так как значение x и y в точке N целые и точка N близка к данной точке M.
возьмем точку N(1,2), так как значение x и y в точке N целые и точка N близка к данной точке M.
Тогда
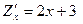 в точке
в точке 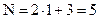
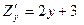 в точке
в точке 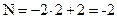
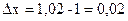
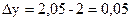
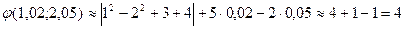
Вычислим точное значение
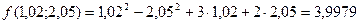
Итак, принимая вместо точного значения 3,9979 значение 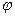 , мы допускаем абсолютную погрешность
, мы допускаем абсолютную погрешность 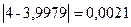 или относительную погрешность
или относительную погрешность 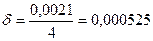
Решите самостоятельно следующие задачи:
20.1 Найти полное приращение и полный дифференциал функции 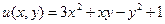
20.2 Найти полный дифференциал функции 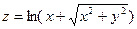
Дата добавления: 2014-12-09; просмотров: 726;
