ЗАДАНИЕ №23
Рассмотрим теперь интегрирование функций нескольких переменных.
Двойным интегралом от функции 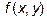 по области D называется предел интегральной суммы при условии, что число элементарных областей n стремится к бесконечности, а наибольший из диаметров элементарных областей стремится к нулю:
по области D называется предел интегральной суммы при условии, что число элементарных областей n стремится к бесконечности, а наибольший из диаметров элементарных областей стремится к нулю:
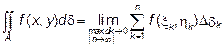
Если функция 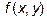 непрерывна в замкнутой области D, то предел интегральной суммы существует и не зависит от способа разбиения области D на элементарные и от выбора точек Рк
непрерывна в замкнутой области D, то предел интегральной суммы существует и не зависит от способа разбиения области D на элементарные и от выбора точек Рк
Если 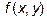 >0 в области D, то двойной интеграл
>0 в области D, то двойной интеграл
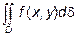
геометрически есть объём цилиндрического тела, ограниченного сверху поверхностью 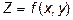 , сбоку цилиндрической поверхностью с образующими, параллельными оси OZ, и снизу областью D плоскости ХОY.
, сбоку цилиндрической поверхностью с образующими, параллельными оси OZ, и снизу областью D плоскости ХОY.
Основные свойства интегралов
1. 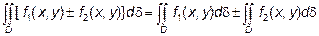
2. 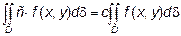 где С – постоянная
где С – постоянная
3. Если область интегрирования D разбита на две области D1 и D2, то
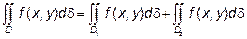
Различают два основных вида области интегрирования:
- Область интегрирования D ограничена слева и справа прямыми х=а и х=в (a<в), а снизу и сверху непрерывными кривыми y=φ1(x) и y=φ2(x)
 , каждая из которых пересекается вертикальной прямой только в одной точке / рис.1/.
, каждая из которых пересекается вертикальной прямой только в одной точке / рис.1/.
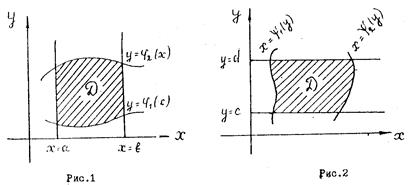
По такой области двойной интеграл вычисляется по формуле:
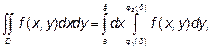
Причем сначала вычисляется внутренний интеграл 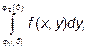 в котором х считается постоянным.
в котором х считается постоянным.
- Область интегрирования D ограничена снизу и сверху прямыми y=c и y=d (c<d) , а слева и справа непрерывными кривыми х=φ1(y) и х=φ2(y)
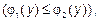 каждая из которых пересекается горизонтальной прямой только в одной точке ( рис. 2).
каждая из которых пересекается горизонтальной прямой только в одной точке ( рис. 2).
В такой области двойной интеграл вычисляется по формуле:
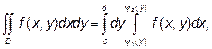
Причем сначала вычисляется интеграл 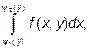 в котором y считается постоянным.
в котором y считается постоянным.
Правые части формул называются двукратными или повторными интегралами. В более общем случае область интегрирования путем разбиения на части сводится к основным.
Подробнее о двойных и тройных кратных интегралах можно прочесть в [5] гл.14 и [1] гл XXVI
Пример 1.Вычислить двойной интеграл: 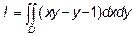 .
.
По области D: y=x2, y=2-x2. Область D изобразить на чертеже.
Решение: Изобразим область D. Кривые, задающие область D представляют собой параболы. Составив из их уравнений систему и решив её, найдём точки их пересечения.
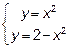

 Итак, точки пересечения парабол(1,1) и (-1,1). Изобразим область D в декартовой системе координат.
Итак, точки пересечения парабол(1,1) и (-1,1). Изобразим область D в декартовой системе координат.
Двойной интеграл в декартовых координатах записывается так: 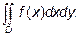 В зависимости от вида области интегрирования двойной интеграл сводится к повторному по разным формулам.
В зависимости от вида области интегрирования двойной интеграл сводится к повторному по разным формулам.
Область D является областью первого вида, х изменяется от -1 до +1, у от у=х2 до у=2-х2, следовательно наш интеграл сводится к следующему повторному интегралу:
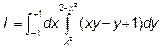
Возьмем внутренний интеграл, считая х – постоянным, то есть рассматривая его как обычный интеграл по переменной у.
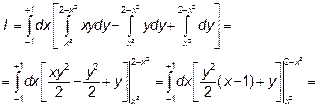

А затем внешний интеграл по переменной х
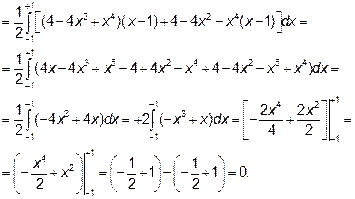
Пример 2.С помощью двойного интеграла найти объем тела, ограниченного поверхностями:
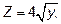 x+y=4, x=0, Z=0.
x+y=4, x=0, Z=0.
Решение : Как было сказано, объем тела с помощью двойного интеграла выражается по формуле:
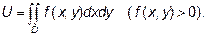

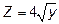 - это цилиндрическая поверхность с образующими, параллельными оси ОХ.
- это цилиндрическая поверхность с образующими, параллельными оси ОХ.
Направляющей служит парабола, точнее одна ветвь параболы


x+y=4 - это плоскость, параллельная оси OZ, пересекающая плоскость ХОУ по прямой,
заданной уравнением x+y=4. Построим ее на том же чертеже.
Уравнения Х=0 и Z=0 задают соответственно координатные плоскости ZOУ и ХОУ.
Итак, нетрудно себе представить, что тело ограничено сверху цилиндрической поверхностью 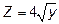 , снизу плоскостью ХОУ, сбоку х=0 и x+y=4.
, снизу плоскостью ХОУ, сбоку х=0 и x+y=4.

Необходимо построить область D.

Область интегрирования D принадлежит одновременно и к первому и ко второму виду.
Будем рассматривать ее как область первого вида. Воспользуемся формулой для области первого вида.
Чтобы правильно расставить пределы интегрирования, нужно помнить, что пределами на внешнем интеграле могут быть только числа( пределы изменения Х ), а на внутреннем, в общем случае, функции. Нужно уяснить, какой кривой ограничена область снизу, и какой – сверху, и записать соответственно правые части уравнений кривых, решенных относительно У, в качестве пределов интегрирования. В качестве подинтегральной функции 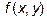 пишем правую часть уравнения
пишем правую часть уравнения 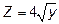 .
.
Получим:
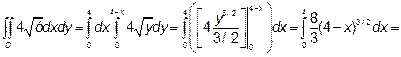
= 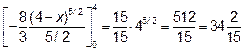
Ответ: 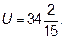 .
.
Решите самостоятельно следующие задачи:
23.1 Измените порядок интегрирования в двойном интеграле 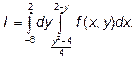
23.2 Вычислить с помощью двойного интеграла в полярных координатах площадь фигуры, ограниченной кривой 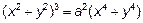
Дата добавления: 2014-12-09; просмотров: 1369;
