ЗАДАНИЕ №22

Следующая задача посвящена нахождению вектора – градиента для функции нескольких переменных.

Подробнее об этом можно прочесть в [4] гл.8 и [1]гл.XXVIII

вектор-градиент обозначается grad u или Ñu.

Пример 1.Даны функция трех переменных 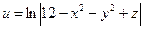, вектор 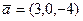и точка .

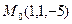Найти: 1) Grad u в точке M₀;

2) производную в точке M₀ по направлению вектора ;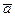

3) наибольшую крутизну поверхности u в точке M₀.

Решение:

1) Вектором градиентом функции трех переменных u(x,y,z) является вектор
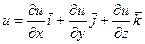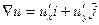grad (или в случае двух переменных)

Найдем частные произведения функции u:

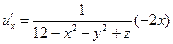
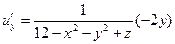
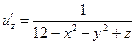
Из определения градиента следует, что эти частные производные являются проекциями вектора-градиента на оси координат. Вычислим значения частных производных в точке M_o.

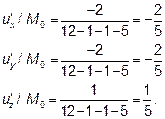
Следовательно вектор-градиент в точке M₀ имеет вид:

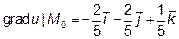
2) Производная по направлению вектора 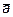вычисляется по формуле 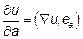, то есть равна скалярному произведению вектора градиента на единичный вектор, совпадающий по направлению с вектором .

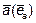Так как 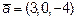, то его длина 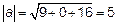и, следовательно, единичный вектор, совпадающий по направлению с 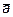, , 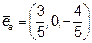используя формулу скалярного произведения в координатной форме 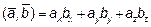, получим

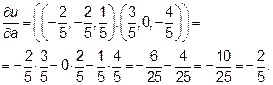
Итак производная функции u по направлению вектор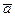а равна .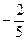

3) Поскольку |grad u| есть наибольшее значение производной 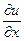в данной точке P, а направление grad u совпадает с направлением луча, выходящего из точки P, вдоль которого функция меняется быстрее всего, то направление градиента есть направление наискорейшего возрастания функции u(x,y,z)

|grad u| = .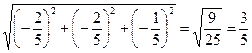

Решите самостоятельно следующие задачи:

22.1 Найти вектор-градиент функции 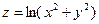в точке (1,1)

22.2 Найти производную функции 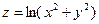в направлении вектора-градиента

Аналогичные задачи можно найти в [3] гл.8