ЗАДАНИЕ №17
Далее разберём задачу о вычислении несобственных интегралов.
Определённый интеграл, который рассматривался в предыдущей задаче, вычисляется при двух предположениях:
1) отрезок интегрирования [a,b] конечен
2) подынтегральная функция на этом отрезке непрерывна
При таких предположениях интеграл называется собственныминтегралом. В том случае, если отрезок интегрирования бесконечен или конечен, но подынтегральная функция на этом отрезке терпит разрыв, интеграл называется несобственныминтегралом.
Несобственный интеграл с бесконечными пределами.
Пусть функция f(x) в промежутке 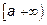 непрерывна. Интегралом от f(x) в пределах между
непрерывна. Интегралом от f(x) в пределах между 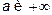 называется предел интеграла, взятого от
называется предел интеграла, взятого от 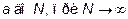 , т.е.
, т.е. 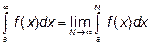
Это несобственный интеграл.
Если конечный предел в правой части существует, то несобственный интеграл называется сходящимся, а функция f(x)- интегрируемой на  . Если этот предел бесконечен или не существует, то интеграл называется расходящимся.
. Если этот предел бесконечен или не существует, то интеграл называется расходящимся.
Интеграл 
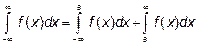 для любого a.
для любого a.
Пример 1.Вычислить 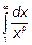
а) p¹1
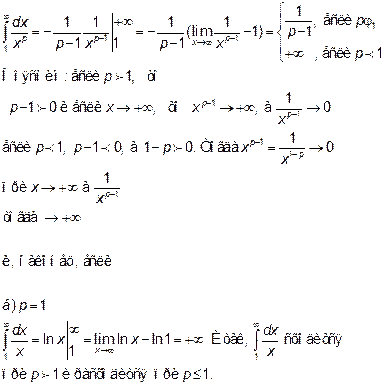
Пример 2.Вычислим несобственный интеграл 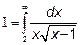 или покажем, что он расходится.
или покажем, что он расходится.
Решение:Найдем неопределённый интеграл 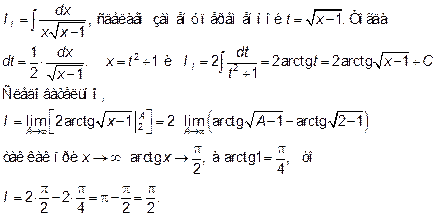
Итак, предел существует, значит, несобственный интеграл I сходится и равен 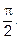
Интеграл 2-го рода.
Если в интеграле 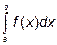 функция f(x) неограниченно возрастает, то есть
функция f(x) неограниченно возрастает, то есть 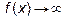 когда x приближается к одному из пределов интегрирования. Когда это происходит при x®a, то
когда x приближается к одному из пределов интегрирования. Когда это происходит при x®a, то 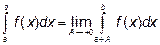 .
.
Если подынтегральная функция перестаёт быть ограниченной внутри отрезка интегрирования, например в точке с то эту точку вырезают:
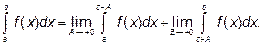
Пример 3.Вычислим 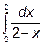
Решение: Когда x®2 подынтегральная функция 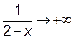 . Точка x=2 особая.
. Точка x=2 особая.
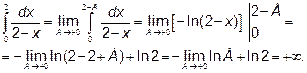
То есть интеграл расходящийся.
Подробнее с несобственными интегралами можно ознакомиться в[1]гл.XIV, [4] гл.11 и найти задачи на эту тему в [3] гл.10
Решите самостоятельно следующие задачи. Вычислить интегралы:
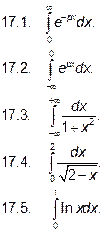
Дата добавления: 2014-12-09; просмотров: 685;
