ЗАДАНИЕ №12
Следующая задача относится к вычислению производных.
Пусть функция y=f(x) определена в некоторой окрестности точки «x».
Производной функции y=f(x) в точке «x» называется предел отношения приращения функции 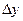 к соответствующему приращению аргумента
к соответствующему приращению аргумента 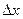 , при стремлении
, при стремлении 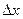 к нулю.
к нулю.
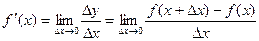
Производная 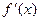 функции f(x) в точке x существует, если f(x) непрерывна в точке x и
функции f(x) в точке x существует, если f(x) непрерывна в точке x и
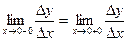
Для отыскания производных элементарных функций используется таблица производных основных элементарных функций и правила дифференцирования.
1. 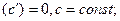
| 10. 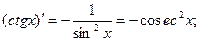
|
2. 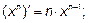
| 11. 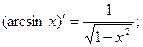
|
3. 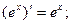
| 12. 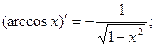
|
4. 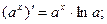
| 13. 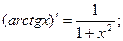
|
5. 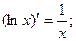
| 14. 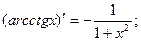
|
6. 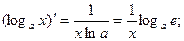
| 15. 
|
7. 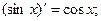
| 16. 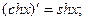
|
8. 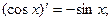
| 17. 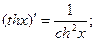
|
9. 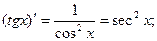
| 18. 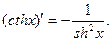
|
Основные правила дифференцирования:
Для дифференцируемых в точке x функций f(x) и g(x) справедливы равенства:

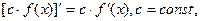
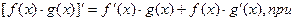
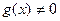
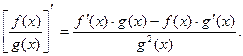
Производная сложной функции 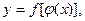 где
где 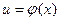 - промежуточный аргумент. Если существуют
- промежуточный аргумент. Если существуют 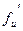 и
и 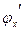 , то
, то
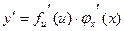 или
или 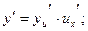
Производная обратной функции. Если для функции y=f(x) существует обратная функция 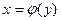 , которая имеет в точке y производную
, которая имеет в точке y производную 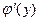 , то
, то
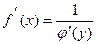 или
или 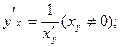
Дифференцирование неявной функции. Пусть уравнение
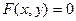
определяет y как неявную функцию от x, т.е. y=f(x) – неизвестная дифференцируемая функция и F(x,y) сложная функция. Дифференцируем по x обе части и получаем уравнение первой степени относительно 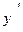 , из которого легко находится
, из которого легко находится 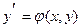 - производная искомой функции.
- производная искомой функции.
Производная параметрически заданной функции x=x(t), y=y(t), 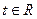 - параметр. Если существуют производные
- параметр. Если существуют производные 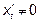 и
и 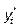 , то
, то
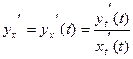
Пример 1.Найти производные 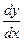 следующих функции:
следующих функции:
а) 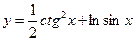 , б)
, б) 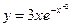 , в)
, в) 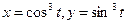
Решение: а) 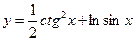 . Наша функция является суммой двух функций. Воспользуемся свойством производной суммы
. Наша функция является суммой двух функций. Воспользуемся свойством производной суммы
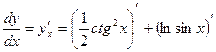
Константу 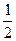 вынесем за знак производной и получим две производные сложных функций:
вынесем за знак производной и получим две производные сложных функций:
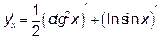
Поскольку внешняя функция в первом слагаемом – степенная, а во втором – натуральный логарифм, то для 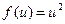 ,
, 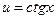 и
и 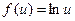 ,
, 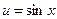 по формуле дифференцирования сложной функции получим:
по формуле дифференцирования сложной функции получим:
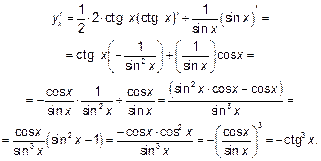
б) 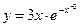 . Здесь мы воспользуемся свойством производной произведения двух функций , где
. Здесь мы воспользуемся свойством производной произведения двух функций , где 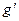 - есть производная сложной функции, внешняя функция которой показательная, а внутренняя – степенная.
- есть производная сложной функции, внешняя функция которой показательная, а внутренняя – степенная.
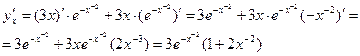
в) 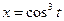 ,
, 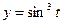 . Производную функции, заданной параметрически, находим, учитывая, что
. Производную функции, заданной параметрически, находим, учитывая, что 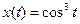 ,
, 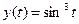 - сложные функции.
- сложные функции.
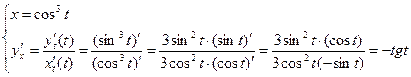
Подробно о производных можно прочесть в [1] гл.9, [4] гл.3 и найти задачи можно в [3] гл.7 §1.
Дата добавления: 2014-12-09; просмотров: 684;
