ЗАДАНИЕ №9
Чтобы решить задачу№9,необходимо уметь выполнять действия над комплексными числами в алгебраической и тригонометрической их формах. Подробно прочитать об этих числах можно в [4] гл7.
Пример 1.Выполнить действия над комплексными числами в алгебраической форме.
Решение: Алгебраической формой комплексного числа называется следующий его вид z=x+iy. Действия над комплексными числами в алгебраической форме производятся как над многочленами вида a+xb. Специфическим приёмом деления комплексного числа на комплексное число является домножение и числителя и знаменателя на комплексно сопряжённое знаменателю число. В результате частное не изменится, но делитель будет вещественным.
Заметим что 
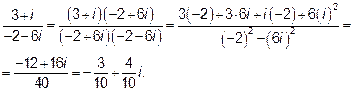
Пример 2.Найти тригонометрическую форму числа  . Найти:
. Найти: 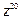
Решение :Выражение вида  называется тригонометрической формойчисла z, где модулем z называют
называется тригонометрической формойчисла z, где модулем z называют  , аргументом z– угол
, аргументом z– угол между радиус-вектором точки zи положительным направлением оси Ох.
между радиус-вектором точки zи положительным направлением оси Ох.

Очевидно, что если |z|= r, arg z = j, то действительная часть числа z Re z = x = r cosj, а мнимая часть числа z Jm z = y = r sin j.
Таким образом, в терминах модуля и аргумента комплексное число можно представить в виде 
Для определения тригонометрической формы комплексного числа z найдём r, 
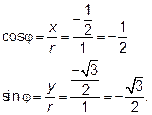
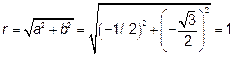
Та как sin и cos угла  отрицательны, делаем вывод, что угол находится в III четверти
отрицательны, делаем вывод, что угол находится в III четверти 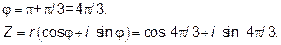
Вычислим по формуле Муавра 
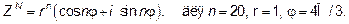
120=1

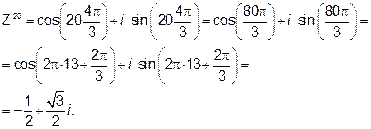
Пример 3.Решить уравнение 
Известно, что корнем n-степени из числа zназывается любое число 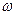 , такое, что
, такое, что  и ω имеет nразличных значений.
и ω имеет nразличных значений.
Решение: если число z представить в тригонометрической форме 
то значения  можно представить формулой
можно представить формулой 
Поскольку все  одинаковы, а аргументы отличаются на 2П/n, то значения
одинаковы, а аргументы отличаются на 2П/n, то значения 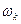 на комплексной плоскости располагаются в вершинах правильного n угольника. Величина
на комплексной плоскости располагаются в вершинах правильного n угольника. Величина  называется главным значением корня
называется главным значением корня

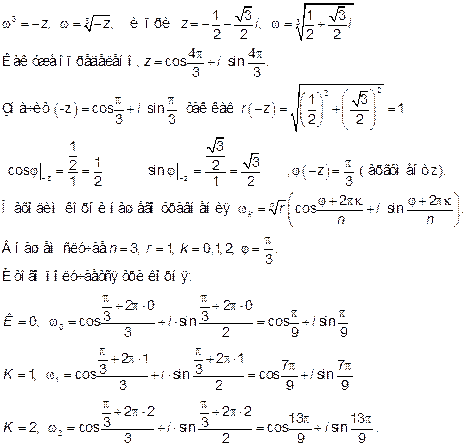
Итак, корнями уравнения будут три единичных вектора, расположенных под углом в 120 градусов друг к другу.
Решить самостоятельно следующие задачи:
9.1 .Найти все значения 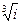
9.2 .Найти все значения 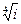
Дата добавления: 2014-12-09; просмотров: 716;
