ЗАДАНИЕ №7. Следующие три задачи относятся только к студентам специальности ЭВМ.

Квадратичной формой действительных переменных 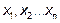называется многочлен второй степени относительно этих переменных, не содержащий свободного члена и членов первой степени. Если 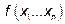- квадратичная форма переменных 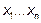, а λ – какое-то действительное число, то .

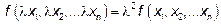Если n=2, то .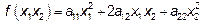

Матрица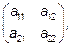

у которой 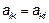, называется матрицей квадратичной формы .

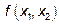Т.к. А – симметричная матрица, то корни λ₁ и λ₂ характеристического уравнения

являются действительными числами.

Пусть 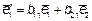и

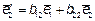
нормированные собственные векторы, соответствующие характеристическим числам λ₁ и λ₂ в ортонормированном базисе 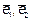. В свою очередь векторы 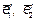образуют ортонормированный базис. Матрица

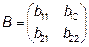
Является матрицей перехода от базиса к базису 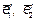. Формулы преобразования координат при переходе к новому ортонормированному базису имеют вид:

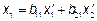
Преобразовав с помощью этих формул квадратичную форму 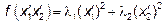, (не содержащую членов с произведениями).

говорят, что форма приведена к каноническому виду.

Пример 1.Приведем к каноническому виду квадратичную форму .

; ; .

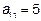Составим характеристическое уравнение

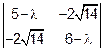=0 или .

; .

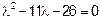Определим собственные векторы

I)

;

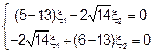
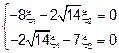
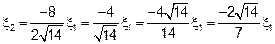Полагая что 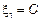, получим , то есть собственный вектор .

II) .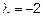

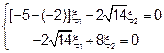
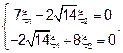
Полагая что 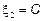, получим 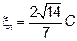, то есть собственный вектор .

Чтобы нормировать векторы u и v, следует принять .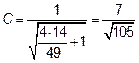

Итак, мы нашли нормированные собственные векторы

где 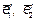- ортонормированный базис, в котором матрица квадратичной формы имеет диагональный вид.

Матрица перехода от ортонормированного базиса к ортонормированному базису 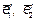имеет вид:

B=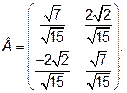

Канонический вид квадратичной формы

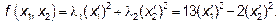
Решите эту задачу самостоятельно:

Задача 7.1. Приведите к каноническому виду квадратичную форму

Подробнее можно об этом прочитать в [2], §23 и найти задачи на эту тему в [3] гл.5 §7.