ЗАДАНИЕ №8
Это заданиеотносится к разделу «линейные операторы»; более подробно о линейных операторах (отображениях, преобразованиях) можно прочитать в [1] гл. 6, [2] §15 и найти решённые задачи этой темы можно в [3] гл. 5 §4.
Если в линейном пространстве R каждому вектору  по некоторому правилу поставлен в соответствие вектор
по некоторому правилу поставлен в соответствие вектор 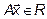 , то говорят, что в пространстве R задан оператор A. Оператор A называется линейным, если для любых векторов
, то говорят, что в пространстве R задан оператор A. Оператор A называется линейным, если для любых векторов 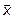 и
и 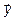 и любого действительного числа λ выполняются равенства:
и любого действительного числа λ выполняются равенства:
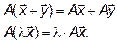
Значит, для того, чтобы проверить, является ли оператор A линейным надо проверить, выполняются ли эти равенства.
Проверим, является ли оператор A линейным в R3
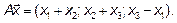
Возьмем два вектора 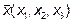 и
и 
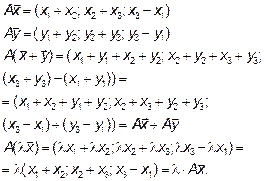
То есть оператор A является линейным, найдем его матрицу.
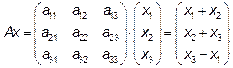
Первая координата произведения получается умножением первой строки на столбец 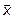 , то есть
, то есть 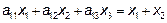 , значит
, значит 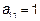 ,
, 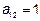 ,
, 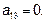
Вторая координата произведения:
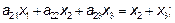

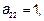
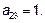
Третья координата произведения:
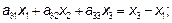

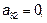
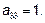
Итак, матрица оператора
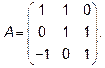
Найдем собственные значения линейного оператора:

(1-λ)·(1-λ)2-1·1=0
(1-λ)3=1
1-λ=1
λ=0
Оператор A имеет собственное значение λ=0 кратности 3.
Для определения координат собственного вектора получаем систему уравнений:
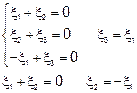

положив
получим:
Собственному числу 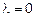 соответствует собственный вектор
соответствует собственный вектор 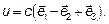
Дата добавления: 2014-12-09; просмотров: 906;
