ЗАДАНИЕ №5

Задача №5 – это задача нахождения обратной матрицы.

Какие операции можно выполнить над матрицами?

Сложение матриц:

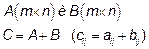
Умножение матрицы на число:

Умножение матриц:

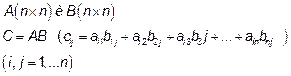
Транспонирование матриц:

То есть элемент матрицы 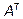находящийся в позиции совпадает с элементом матрицы А, находящимся в позиции . Таким образом строки матрицы А переходят в столбцы 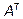, а столбцы– в строки.

Нахождение определителя (для квадратных матриц):

Для нахождения определителя третьего порядка мы пользовались в предыдущих задачах формулой:

,

Т.е. умножили элементы первой строки на определители, которые останутся от исходного определителя третьего порядка, если вычеркнуть этот элемент вместе со своей строкой и столбцом.

Определителем матрицы n-го порядка

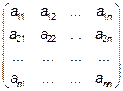называется число D

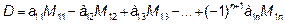
Где 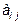– элементы первой строки, знак совпадает со знаком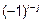

– минор – то есть определитель, матрицы порядка n-1, полученной вычеркиванием i-ой строки и j-го столбца.

Таким образом

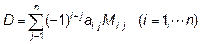– формула разложения определителя по i-ой строке.

Число назовем алгебраическим дополнением элемента 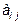. И тогда формулу определителя можно написать в виде:

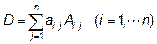
Нахождение обратной матрицы (если ):

, где 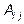– алгебраическое дополнение элемента

Для обратной матрицы

, где Е – единичная матрица

.

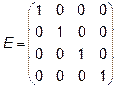Можно построить обратную матрицу методом Жордана. Для этого следует составить расширенную матрицу (А/Е). Если подвергнуть строки этой матрицы элементарным преобразованиям (сложение и умножение на число) с целью получить на месте матрицы А единичную матрицу Е, то на месте матрицы Е получится – обратная к А.

Пример 1.Вычислим матрицу обратную матрице .

Решение. Вычисляем определитель матрицы А

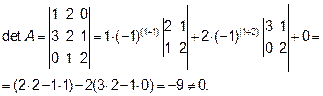
Следовательно, матрица А^-1 существует.

Алгебраические дополнения элементов а_ji исходной матрицы вычисляем по столбцам матрицы А

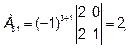
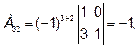
Записываем их в строки матрицы А^-1

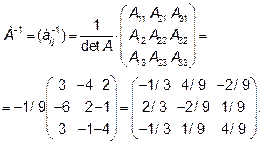
Делаем проверку:

, ,

,

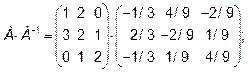
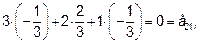
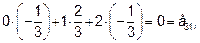
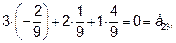
В самом деле:

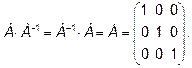
Проверим наши вычисления по методу Жордана.

Составим расширенную матрицу

B =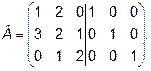

Первый столбец

Наша цель – чтобы первый столбец выглядел так , т.е. надо уничтожить тройку во второй строке. Для этого первую строку умножаем на 3 и вычитаем из второй

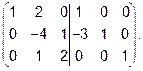
Второй столбец

Теперь надо, сделать второй столбец таким же, как второй столбец матрицы Е, т.е надо чтобы второй столбец был таким .

Для этого вторую строку умножим на

.

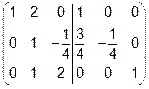Теперь надо уничтожить 2 в первой строке и 1 в третьей строке.

Умножаем вторую строку на 2 и вычитаем из первой. Результат записываем на место первой строки. Вторую строку оставляем на своем месте. Из третьей строки вычитаем вторую строку, результат записываем на место третьей строки.

.

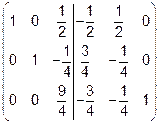Третий столбец

Третий столбец у единичной матрицы должен быть таким , то есть все три строки придется менять. Разделим третью строку на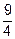

.

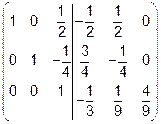Теперь уничтожим в первой строке. Для этого третью строку умножим на и вычтем из первой. Результат запишем на место первой строки.

Теперь в третьем столбце от столбца единичной матрицы отличается только элемент второй строки. Это . Чтобы на этом месте был ноль, добавим ко второй строке третью, умноженную на . Результат впишем на место второй строки.

.

Теперь сократим все дроби, где это возможно

.

Действительно, мы получили матрицу .

Решите самостоятельно следующие задачи: