ЗАДАНИЕ №3
Для решения третьей задачи потребуются следующие понятия о кривых второго порядка: Пусть на плоскости имеется прямоугольная декартова система координат. Как было видно в предыдущей задаче, множество точек плоскости, удовлетворяющих равенству 
=0 является линией.
В примере №2 уравнения были линейными( т.е.функция 
являлась многочленом первой степени), линия- прямой линией; то есть линиями первого порядка являлись прямые линии. В качестве функции может выступать и многочлен второй степени
такое уравнение – уравнение линии второго порядка.
ЭЛЛИПС
Если уравнение имеет вид
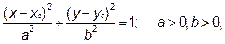
то кривая называется эллипсом (каноническое уравнение эллипса). Точка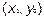 
-центр эллипса. Точки (± 
,0),(0, ± 
) называются вершинами эллипса.
( 
< 
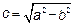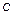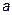) – расстояние от центра до фокусов
Если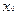 
= 
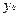=0, то центр эллипса совпадает с началом координат и точки (- 
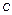,0) и ( 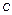,0) –левый и правый фокусы эллипса.
Число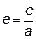 
называется эксцентриситетом эллипса.
ГИПЕРБОЛА
Если уравнение имеет вид
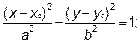
>0, 
>0
кривая называется гиперболой ( каноническое уравнение гиперболы)
Точка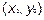 
- центр гиперболы, Точки (± ,0)-вершины гиперболы, При 
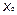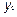=0, 
=0,
Прямые 
= ± 
асимптоты гиперболы.
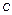, >0. Точки (- 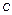,0) и ( 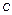,0) фокусы гиперболы.
ПАРАБОЛА
Если уравнение имеет вид:
, где 
>0, то линия называется параболой ( каноническое
уравнение параболы)
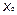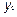, -координаты вершины параболы; При 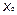= =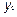0 ( 
,0 ) - фокус параболы ; прямая
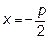- директриса параболы.
На плоскости может быть введена не только декартова прямоугольная , но и полярная система координат.
Зададим точку О -полюс, ось Z содержащую точку О и единицу длины оси Z.
Возьмем произвольную точку М плоскости. Её положение на плоскости определяется двумя числами – расстоянием r от О до М (полярный радиус) и отсчитываемым против часовой стрелки углом φ между лучом OM и лучом оси (полярный угол). Если поместить начало координат декартовой прямоугольной системы в полюс, то координаты будут связаны следующим образом.
Пример 1.Пусть в задаче №3
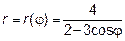
Построим заданную линию по точкам в полярной системе координат. В начале определим область допустимых значений (ОДЗ) независимой переменной φ. По определению полярной системы координат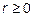 
и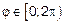 
.Точке r = 0 соответствует полюс 0.
По условию задач угол φ может меняться от 0 до 2π. Поэтому наибольшие размеры ОДЗ таковы 
. При этом r>0 (r 
0), т.к. числитель соответствующей дроби 4>0. отсюда знаменатель этой дроби также должен удовлетворять неравенству
2-3cos φ > 0 или cos φ < 2/3.
Решаем последнее неравенство
cos φ = 2/3 
0,667;
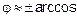0,667 +2πk, k 
N; φ = 
.
В промежуток 
попадают два значения φ1= 
и φ2 = - 
.
Отсюда для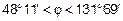 
cos φ<2/3.
Следовательно допустимые значения φ принадлежат промежутку от 3π/8 до 13π/8, т.е. ОДЗ: 
.
Результаты расчетов заносим в таблицу
| φ | 3π/8 | π/2 | 5π/8 | 6π/8 | 7π/8 | π | 9π/8 | 10π/8 | 11π/8 | 12π/8 | 13π/8 |
| cosφ | 0.38 | -0.38 | -0.71 | -0.92 | -1 | -0.92 | -0.71 | -0.38 | 0.38 | ||
| r | 4.75 | 1.27 | 0.97 | 0.84 | 0.8 | 0.84 | 0.97 | 1.27 | 4.75 |
Строим чертеж ,откладывая на луче , проведенном из полюса О под определенным углом φ, соответствующие значения радиус-вектора r из таблицы
 |
rl(φ)
Для перехода к системе 0ху воспользуемся формулами. Имеем, следовательно
r (2-3cos φ)=4, 
Определяем ОДЗ для х. Из ОДЗ : для φ 
>0.
Следовательно 3х+4>0. Отсюда ОДЗ: х>-4/3.
Возводим правую и левую части равенства в квадрат и выделяем полный квадрат для переменной х:
4х2+4у2=9х2+24х+16;
(5х2+24х)-4у2+16=0;
5(х2+2 
;
(х+12/5)2-4/5у2-144/25+16/5=0;
(х+12/5)2-4у2/5=64/25
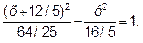
Окончательно получаем уравнение гиперболы
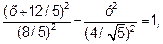х > - 
с центром в точке С(-12/5;0), а = 8/5, b = 4/ 
.
Находим координаты фокусов, уравнения асимптот и эксцентриситет. Для этого систему координат 0ху параллельно перенесем в точку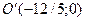 
. Заменяя переменные
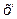=х+12/5, 
=у,
получим в новой системе координат 
уравнение гиперболы с центром в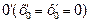 
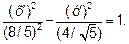
Получим координаты фокусов, уравнения асимтот и эксцентриситет гиперболы:
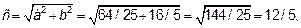
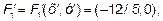
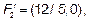
или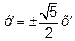 
, 
Переходим в старую систему координат. Имеем:
.
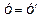Следовательно:
F1(x;y)=F1( 
=F1(-24/5;0);
F2(0;0), у = +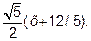 
Совмещаем начало О системы координат Оху с полюсом, отмечаем координаты фокусов F1 и F2, проводим асимптоты и строим пунктиром левую ветвь гиперболы, т.к. точки гиперболы в полуплоскости слева от прямой х=-4/3 не удовлетворяют ОДЗ х>-4/3.
Более подробное описание кривых второго порядка смотрите в [1] гл.3; в [2] §24.
В случае если уравнение не подходит под один из перечисленных выше частных случаев линии второго порядка требование задачи «назвать линию» следует опустить.
Решение аналогичных задач можно найти в [3] гл.1 §3.
Решите самостоятельно задачи:
3.1 Привести к простейшему виду уравнение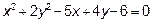 
3.2 Уравнение асимптот гиперболы 
и 
, а расстояние между фокусами 
. Найти уравнение гиперболы.
Дата добавления: 2014-12-09; просмотров: 823;