ЗАДАНИЕ №1.
Для решения контрольной работы №1 по математике и контрольной работы №1 по курсу алгебра и геометрия следует изучить разделы векторной алгебры, линейной алгебры и аналитической геометрии любых учебников. Для решения задач первой контрольной понадобятся следующие понятия и факты:
Для решения первой задачи:
Определители 2 и 3 порядков
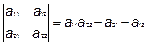 -определитель 2-го порядка
-определитель 2-го порядка
Заметим, что у элемента определителя 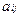
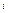 -номер строки, а
-номер строки, а 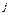 -номер столбца
-номер столбца
 -
-
- определитель 3 порядка
Векторы и действия над ними.
В декартовой прямоугольной системе координат вектор  (или
(или 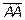 ) имеющий начало в точке А(3,4,0) и конец в точке В(5,7,5) имеет следующие координаты
) имеющий начало в точке А(3,4,0) и конец в точке В(5,7,5) имеет следующие координаты
 (5-3; 7-4;5-0) или
(5-3; 7-4;5-0) или 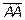 (2,3,5)
(2,3,5)
Векторы можно складывать и если 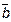 =
= 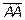 +
+ 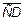 , где
, где 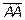 (2,3,5) а
(2,3,5) а 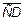 (4,5,6) то
(4,5,6) то 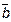 (2+4;3+5;5+6) =
(2+4;3+5;5+6) = 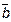 (6,8,11)
(6,8,11)
Можно умножить вектор на число, например если  (2,3,5) умножить на (-2) получим вектор -2
(2,3,5) умножить на (-2) получим вектор -2  (-4,-6,-10)
(-4,-6,-10)
Длина (модуль) вектора обозначается 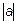 и считается по формуле
и считается по формуле
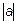 =
= 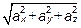
для  (2,3,5)
(2,3,5)
|  |=
|= 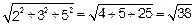
Итак, мы имеем заданную в пространстве декартову прямоугольную систему координат 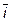 ,
, 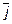 ,
, 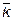 - единичные векторы (орты) положительных направлений осей
- единичные векторы (орты) положительных направлений осей 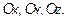 И когда мы пишем, что
И когда мы пишем, что  (2,3,5) это означает, что
(2,3,5) это означает, что  =
= 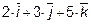
Тройку векторов 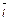
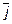
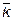 называют ортонормированным координатным базисом.
называют ортонормированным координатным базисом.
2,3,5 - координаты вектора  , а
, а
2 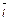 , 3
, 3 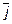 , 5
, 5 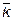 - компоненты вектора
- компоненты вектора  .
.
Пусть имеем два вектора  (2,3,5) и
(2,3,5) и 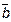 (6,8,11).
(6,8,11).
Скалярным произведением вектора  навектор
навектор 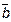 называется число (
называется число (  ,
, 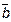 ) =
) = 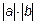
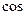
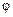 , где
, где 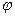 угол между
угол между  и
и 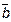 .
.
В координатной форме
(  ,
, 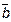 ) =
) = 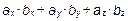 - т.е. сумме произведений одноимённых координат
- т.е. сумме произведений одноимённых координат
= 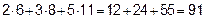
Скалярное произведение можно использовать, чтобы найти длину вектора.
Скалярный квадрат
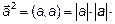
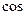
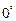 =
= 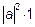
таким образом
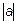 =
= 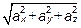 =
= 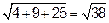
С помощью скалярного произведения можно найти угол между двумя векторами
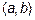 =
= 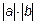
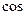
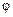 , значит
, значит
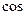
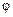 =
= 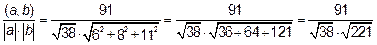
Векторным произведением  на
на 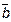 называется вектор, обозначаемый
называется вектор, обозначаемый 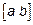 или
или 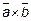
и такой, что:
1) длина |[a, b]| = |a|·|b|·sin 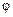 –т.е. численно равно площади параллелограмма, построенного на векторах
–т.е. численно равно площади параллелограмма, построенного на векторах  и
и 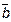
2) 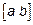 перпендикулярен плоскости векторов
перпендикулярен плоскости векторов  и
и 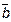
3) вектора  ,
, 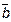 , и
, и 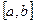 составляют правую тройку, т.е. расположены как большой, указательный и средний палец правой руки.
составляют правую тройку, т.е. расположены как большой, указательный и средний палец правой руки.
Координатная форма векторного произведения
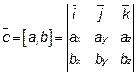
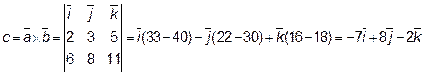
или 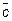 (-7,8,-2)
(-7,8,-2)
Смешанное произведение трех векторов  ,
, 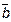 и
и 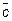 обозначается
обозначается 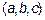 и равно
и равно 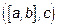 , то есть векторной произведение
, то есть векторной произведение  на
на 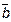 скалярно умножено на
скалярно умножено на 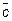 (значит, это число- скаляр)
(значит, это число- скаляр)
Численно модуль смешанного произведения равен объему параллелепипеда, построенного на векторах  ,
, 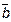 и
и 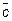 .
.
Координатная форма смешанного произведения
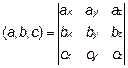
Поскольку в случае компланарности векторов объем соответствующего параллелепипеда равен нулю, то условием компланарности является равенство нулю их смешанного произведения 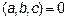
Плоскость и прямая в пространстве.
Рассмотрим произвольную плоскость и на ней вектор-нормаль 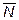 , то есть вектор, перпендикулярный плоскости и фиксированную точку
, то есть вектор, перпендикулярный плоскости и фиксированную точку 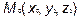 .Возьмем текущую точку
.Возьмем текущую точку 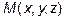 ,координаты которой меняются так, что точка
,координаты которой меняются так, что точка  остается в плоскости, таким образом вектор
остается в плоскости, таким образом вектор  также всегда, при любых движениях точки
также всегда, при любых движениях точки  лежит в плоскости.
лежит в плоскости.
Итак, вектор 
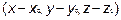 лежит в плоскости, а вектор
лежит в плоскости, а вектор 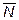
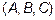 ей перпендикулярен. Тогда их скалярное произведение равно нулю:
ей перпендикулярен. Тогда их скалярное произведение равно нулю:
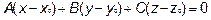 , или
, или 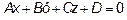 , где
, где 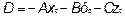
Это общее уравнение плоскости.
Если 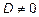 , то разделив все члены уравнения на
, то разделив все члены уравнения на 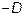 получим уравнение плоскости в отрезках
получим уравнение плоскости в отрезках
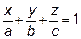
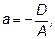
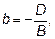
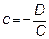 .
.
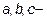 абсцисса, ордината и аппликата точек пересечения плоскости с осями
абсцисса, ордината и аппликата точек пересечения плоскости с осями 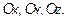
Рассмотрим три заданные точки в пространстве 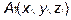 ,
, 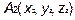 и
и 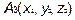 .
.
Как известно, три точки определяют плоскость. Введём текущую точку 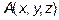 , координаты которой меняются, но она не выходит за рамки плоскости. Рассмотри три вектора
, координаты которой меняются, но она не выходит за рамки плоскости. Рассмотри три вектора 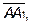
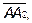
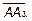 Все они лежат в плоскости
Все они лежат в плоскости 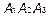 , то есть они компланарны и их смешанное произведение равно нулю.
, то есть они компланарны и их смешанное произведение равно нулю.
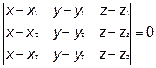
Это уравнение плоскости, проходящей через три заданные точки.
Рассмотрим в пространстве прямую. Её можно задать, задав фиксированную точку, через которую она проходит и задав её направление при помощи вектора.
Итак, напишем уравнение прямой, проходящей через заданную точку 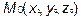 и параллельной направляющему вектору
и параллельной направляющему вектору 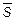
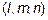 . Опять возьмем текущую точку на прямой, т.е. точку, координаты которой меняются так, чтобы она не вышла за пределы этой прямой
. Опять возьмем текущую точку на прямой, т.е. точку, координаты которой меняются так, чтобы она не вышла за пределы этой прямой 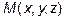 . Вектор
. Вектор  лежит на прямой и, значит, коллинеарен вектору
лежит на прямой и, значит, коллинеарен вектору 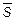 .
.
Если вектора коллинеарны, то их координаты пропорциональны.
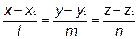 - это и есть канонические уравнения прямой в пространстве.
- это и есть канонические уравнения прямой в пространстве.
Обозначим отношение
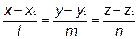 за
за 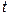
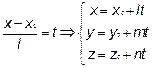
Это параметрические уравнения прямой.
Более подробно этот материал можно найти в  , главы 1 и 2; в
, главы 1 и 2; в  §1,2,5,6,9,10,12,13; в
§1,2,5,6,9,10,12,13; в  главы 1,2,3 можно найти похожие задачи.
главы 1,2,3 можно найти похожие задачи.
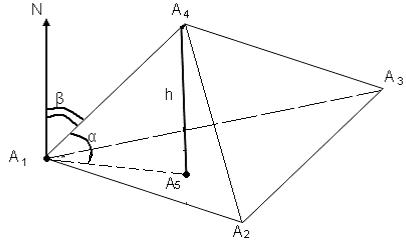
Пример 1.Задана пирамида с вершинами 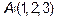 ,
, 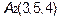 ,
, 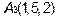 ,
,  .
.
Зная координаты начала и конца вектора 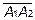 , мы можем найти его координаты:
, мы можем найти его координаты:
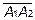
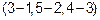 или
или 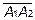
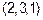
Аналогично найдем 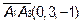
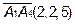
1. Теперь найдем угол 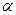 между ребром
между ребром 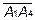 и гранью
и гранью 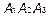 .
.
Вообще говоря, найти угол между прямой и плоскостью, а угол 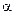 как раз и является углом между прямой
как раз и является углом между прямой 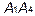 и плоскостью
и плоскостью 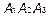 ,- это угол между прямой и её проекцией на плоскость- задача непростая. Угол
,- это угол между прямой и её проекцией на плоскость- задача непростая. Угол 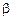 найти проще, а ведь в сумме они составляют
найти проще, а ведь в сумме они составляют 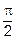 .
.
Значит, найдя 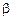 , найдем и
, найдем и 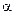 =
= 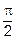 -
- 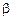 .
.
Итак, ищем 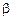 : это угол между вектором-нормалью
: это угол между вектором-нормалью 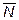 к плоскости
к плоскости 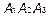 и вектором
и вектором 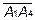 .
.
Отыщем сначала 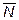 . Какой вектор мы можем выбрать в качестве перпендикуляра к плоскости
. Какой вектор мы можем выбрать в качестве перпендикуляра к плоскости 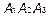 ? Векторное произведение любых двух векторов, лежащих в плоскости, перпендикулярно плоскости. Возьмем векторное произведение
? Векторное произведение любых двух векторов, лежащих в плоскости, перпендикулярно плоскости. Возьмем векторное произведение 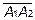
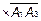 .
.
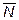 =
= 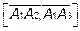 =
= 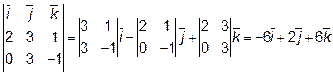
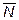 =
= 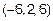
Нас интересует угол 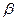 между
между 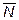 =
= 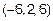 и
и 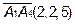 .
.
Скалярное произведение 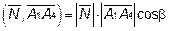
следовательно
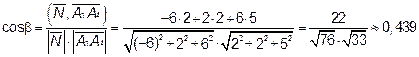
Если 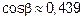 , то
, то 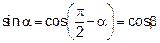
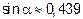
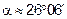 - угол между ребром пирамиды и гранью.
- угол между ребром пирамиды и гранью.
2. Найдем площадь грани 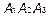 .
.
Площадь грани- это площадь треугольника 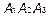 и половина площади параллелограмма, построенного на векторах
и половина площади параллелограмма, построенного на векторах 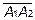 и
и 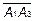 .
.
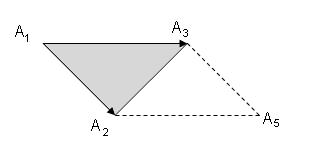
Но мы знаем из определения векторного произведения, что длина вектора 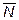 =
= 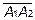
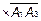 численно равна площади этого параллелограмма. Длину вектора
численно равна площади этого параллелограмма. Длину вектора 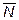 мы считали в пункте 1 и она равна
мы считали в пункте 1 и она равна 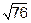 .
.
Итак площадь грани 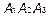 =
= 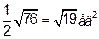
3. Найдем объем пирамиды;
Объем пирамиды равен 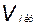 =
= 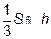
Если отбросить коэффициент  , то получим
, то получим 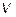 =
= 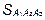
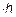 -объем призмы, в основании которой лежит
-объем призмы, в основании которой лежит 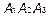 , т.е. объем пирамиды равен
, т.е. объем пирамиды равен  объема призмы
объема призмы 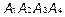 .
.
А объем параллелепипеда, основанием которого является параллелограмм 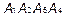 в 2 раза больше объема призмы следовательно, объём пирамиды - это
в 2 раза больше объема призмы следовательно, объём пирамиды - это 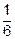 объема параллелепипеда.
объема параллелепипеда.
Но объем данного параллелепипеда численно равен модулю смешанного произведения векторов, на которых построен параллелепипед
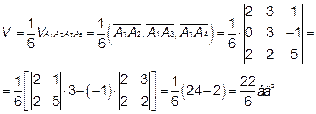
4. Найдем уравнения прямой 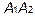 - это уравнения прямой, проходящей через заданную точку
- это уравнения прямой, проходящей через заданную точку 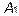 в направлении , заданном вектором
в направлении , заданном вектором 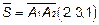 . Итак, пишем уравнение прямой, проходящей через точку А1 (1,2,3) в направлении вектора
. Итак, пишем уравнение прямой, проходящей через точку А1 (1,2,3) в направлении вектора 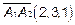
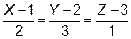
5. Уравнение плоскости 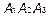 :
:
У нас имеется три точки, лежащие в интересующей нас плоскости, значит используем уравнение плоскости, проходящей через 3 точки:
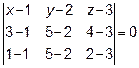
или
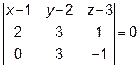
Раскладываем определитель по первой строке
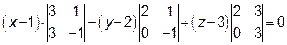
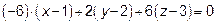
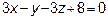
6. Находим уравнения высоты, опущенной из вершины 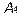 на грань
на грань 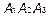 .
.
Раз эта прямая-высота – она перпендикулярна плоскости 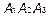 , значит в качестве направляющего вектора прямой можно взять вектор
, значит в качестве направляющего вектора прямой можно взять вектор 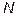 , перпендикулярный
, перпендикулярный 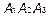 .
.
Высота опущена из вершины 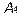 - значит искомая прямая проходит через точку
- значит искомая прямая проходит через точку 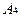 .
.
Итак, пишем уравнения прямой, проходящей через заданную точку 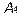 (3,4,8) в направлении заданного вектора
(3,4,8) в направлении заданного вектора 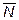 (-6,2,6).
(-6,2,6).
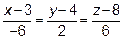
или
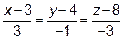
Наконец, найдем координаты точки 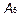 пересечения высоты с нижней гранью.
пересечения высоты с нижней гранью.
То есть точку пересечения прямой 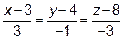 и плоскости
и плоскости 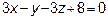
Перейдем к параметрическому виду уравнений прямой:
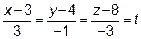
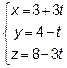
и подставим 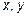 и
и 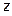 в уравнение плоскости:
в уравнение плоскости:
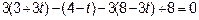
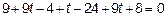
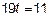
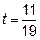
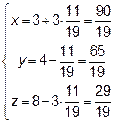
Итак, высота пирамиды пересекается с нижней гранью в точке 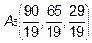 .
.
Дата добавления: 2014-12-09; просмотров: 760;
