ЗАДАНИЕ №4

Для решения задачи № 4 следует иметь понятие о базисе.

Система из n линейно независимых векторов в n-мерном пространственазывается базисом. Векторы называются линейно независимыми, если равенство

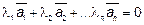
(линейная комбинация этих векторов равна 0) выполняется только при нулевых значениях коэффициентов 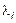– всех 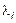при i=1,2…n.

Если это равенство имеет место при условии, что хотя бы один из коэффициентов 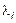отличен от нуля, то система векторов называется линейно зависимой.

В n-мерном пространстве линейно независимая система векторов не может содержать более n векторов.

Пусть задана система из n линейных уравнений с n неизвестными

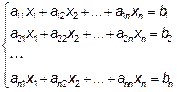
Матрица системы – набор из чисел-коэффициентов системы, так как число строк матрицы равно числу столбцов матрица называется квадратной.

Её определитель (для случая, когда n=3):

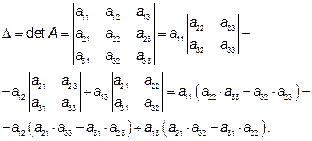
-определитель разложен по первой строке. Как определяются определители высших порядков, можно узнать в указанных ниже учебниках или в следующем разделе.

Итак, если определитель системы , то система имеет единственное решение , которое можно найти по формулам Крамера

Где определитель матрицы системы, а 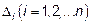определитель матрицы, полученной из матрицы системы А заменой i-го столбца на столбец свободных членов .

Пример 1.Решим задачу разложения вектора по базису:

Пусть даны вектора

Решение.: Покажем в начале, что векторы 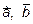и 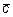образуют базис. Система векторов образует базис, если эти векторы линейно независимы, а соответствующее векторное уравнение

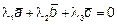
Обращается в тождество только при λ₁=λ₂=λ₃=0.

Используя координаты векторов 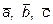, составим систему линейных уравнений, эквивалентную векторному уравнению

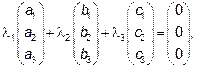
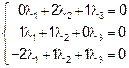
Вычисляем определитель Δ данной системы

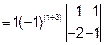=1(-1)-1(-2)=1.

Так как Δ 0, то система имеет только нулевое решение (λ₁,λ₂,λ₃) =(0,0,0). Это следует из того факта, что при b_i =0 все определители при неизвестных в формулах Крамера равны нулю Δ₁= Δ₂ =Δ₃ = 0.

Следовательно, векторы 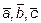образуют базис.

Найдем координаты вектора в базисе 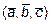. Четыре вектора в трехмерном пространстве всегда линейно зависимы, т.е. вектор есть линейная комбинация векторов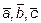

Аналогично предыдущему случаю составим систему уравнений для определения координат λ₁,λ₂,λ₃ вектора в базисе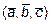

Определитель системы совпадает с определителем системы и не равен нулю Δ=1 0. Следовательно, система имеет единственное решение. По формулам находим λ₁,λ₂ и λ₃

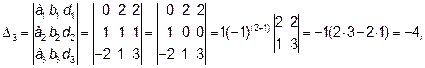
λ₁=Δ₁/Δ=-2/1=-2, λ₂=Δ₂/Δ=3/1=3, λ₃=Δ₃/Δ=-4/1=-4,

Итак, разложение вектора по базису 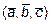имеет вид:

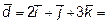Если векторы заданы в базисе , то в этом базисе вектор имеет координаты (2;1;3).

Студенту рекомендуется самостоятельно нарисовать векторы в пространстве R³ и сравнить полученные значения λ_i cо значениями, полученными графически.

Следующую задачу решите самостоятельно:

<3 4 567 8 9 >

Дата добавления: 2014-12-09; просмотров: 914;