ЗАДАНИЕ №10. Для решения контрольной работы №2 по математике или контрольной работы №1 по математическому анализу (для специальности ЭВМ) надо изучить разделы

Для решения контрольной работы №2 по математике или контрольной работы №1 по математическому анализу (для специальности ЭВМ) надо изучить разделы, посвященные пределам функции одной переменной и ее производной.

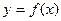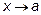Пределом функции при называется число «а» такое, что для любого 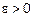можно найти такое число 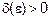, что для любого «x» из промежутка будет выполняться неравенство 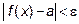. Имеют место следующие свойства пределов: при , имеющие место и при :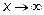

если существуют и не бесконечны 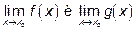, то

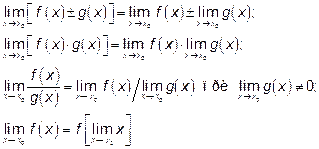
и следующие замечательные пределы

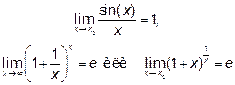
Решим задачи, подобные задачам из контрольной работы:

Пример 1. Найти предел L=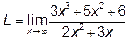

Решение: Имеем неопределённость вида .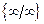

Если к такой неопределённости сводится предел отношения двух

многочленов, при 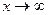следует в числителе и в знаменателе дроби вынести за

скобки самую высокую входящую в них степень аргумента, а затем сократить дробь.

Вынесем за скобки в числителе и знаменателе старшую степень

аргумента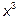

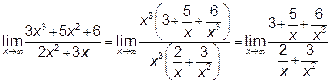
Так как и при 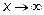, то предел числителя при

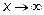равен 3. Предел знаменателя равен 0. Следовательно, предел

дроби равен .

Ответ: L=

Пример 2.Найти .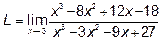

Решение : Здесь неопределённость вида 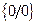.Если к такой

неопределённости сводится предел отношения двух многочленов при

, нужно и в числителе и в знаменателе выделить критический

множитель (x-x₀) и сократить на него числитель и знаменатель дроби.

Выделяем критический множитель (x-3)

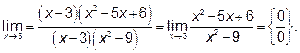
Опять возникла та же неопределённость. Действуя аналогично,

получаем:

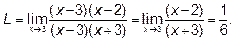
Ответ: .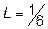

Пример 3.Найти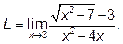

Решение : Неопределённость . В этом случае нужно либо в

числителе, либо в знаменателе дроби избавиться от иррациональных

выражений, которые в точке 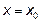обращаются в нуль.

Чтобы раскрыть эту неопределённость, умножим и разделим дробь

на выражение, сопряжённое числителю.

.

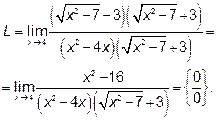Теперь неопределённость создаёт критический множитель .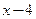

Выделим его в числителе и знаменателе дроби, а затем сократим на него

числитель и знаменатель.

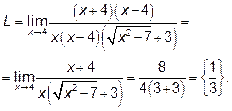
Ответ: L= .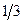

Пример 4.Найти пределыа) 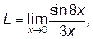б) .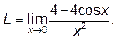

Решение: Неопределённость вида .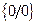

а) При 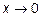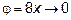. Умножая и числитель и знаменатель

дроби на 8, приведём заданный предел к первому замечательному пределу .

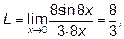
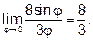
Иногда для раскрытия неопределённости приходится предварительно

применять тригонометрические формулы . В случае б) в числителе

воспользуемся формулой 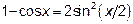и получим

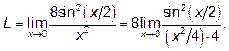
Полагая 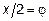и учитывая, что 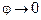при 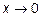, окончательно получим

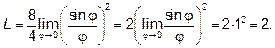
Ответ: а) 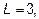, б) .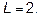

Пример 5.Найти предел .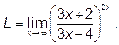

Решение : Неопределённость вида 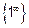.Для раскрытия этой неопределенности

используется второй замечательный предел.

Выделяем в круглых скобках целую часть

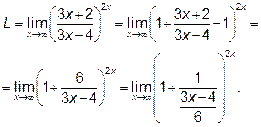
Обозначим 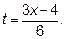. Если 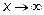, то и 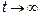. Далее показатель степени

умножаем и делим на .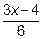

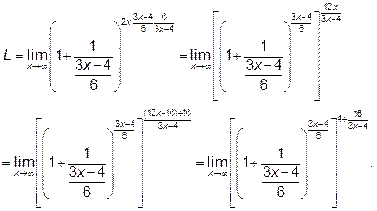
Делаем замену переменно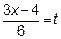й и 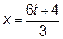. Находим предел

показателя степени

.

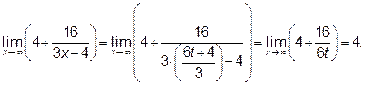
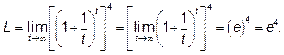Ответ: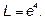

Более подробно о пределах функции можно почитать в [4] глава 2; [1] глава 8 и задачи о пределах можно найти в [3] гл.6 §4.