Характеристическая функция .

Свободная энергия Гельмгольца F.

.

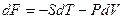Характеристическая функция .

Свободная энергия Гиббса G.

.

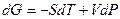Характеристическая функция .

Функции 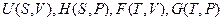называют также термодинамическими потенциалами. Дадим определение термодинамического потенциала.

Термодинамическим потенциалом называется характеристическая функция, убыль которой в обратимом процессе, идущем при постоянстве значений соответствующей пары параметров, равна максимальной полезной работе.

Термодинамические потенциалы стремятся к минимуму при движении системы к равновесию. Перепишем компактно выражения дифференциалов четырёх термодинамических потенциалов:

,

, (***)

,

.

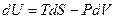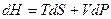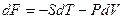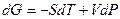Формулы (***) составляют основу для получения термодинамических соотношений, которые связывают термодинамические величины друг с другом и с экспериментально определяемыми параметрами. Такие соотношения можно получать различными способами. Например, имеется выражение для полного дифференциала вида

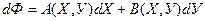
тогда справедливы следующие уравнения:

, ,

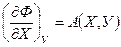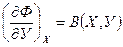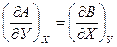
Используя () и () можно получить целый ряд полезных соотношений между термодинамическими величинами.

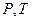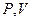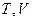Энтропию обычно рассматривают как функцию переменных ; или . Записав выражение для полного дифференциала, находят соотношения между энтропией и экспериментально определяемыми параметрами системы.