Функция, её график и свойства. Основные элементарные функции
Одним из основных математических понятий является понятие функции. В современном представлении функция - это соответствие между элементами двух множеств.
Определение.Пусть даны два непустых множества X и Y. Соответствие f, которое каждому элементу х Î X сопоставляет один и только один элемент y Î Y, называется функцией и записывается y = f(x), х Î X или f : X ® Y. Говорят ещё, что функция f отображает множество X на множество Y.
Множество X называется областью определения функции f и обозначается 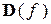 . Множество всех y Î Y называется множеством значений функции f и обозначается
. Множество всех y Î Y называется множеством значений функции f и обозначается 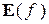 .
.
Пусть задана функция f : X ® Y.
Если элементами множеств X и Y являются действительные числа (т.е. XÌ R и YÌ R), то функция f называется числовой функцией. В дальнейшем будем изучать (как правило) числовые функции, для краткости будем именовать их просто функциями и записывать y = f (x).
Произвольный элемент х Î X называется аргументом или независимой переменной, а y - функцией или зависимой переменной (от х). Относительно самих величин х и у говорят, что они находятся в функциональной зависимости. Иногда функциональную зависимость у от х пишут в виде у = у(х), не вводя новой буквы (например, f ) для обозначения зависимости.
Частное значение функции f (x) при х = а записывают так: f (а), у(а),  . Например, если
. Например, если 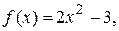 то f (0) = -3,
то f (0) = -3, 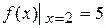 .
.
Графиком функции y = f (x) называется множество всех точек плоскости Оху с координатами (х, f (x)), х Î C, а f (x) - соответствующее значение функции.
Чтобы задать функцию y = f (x), необходимо указать правило, позволяющее, зная х, находить соответствующее значение у.
Наиболее часто встречаются три способа задания функции: аналитический, табличный, графический.
Аналитический способ: функция задаётся в виде одной или нескольких формул или уравнений.
Например:
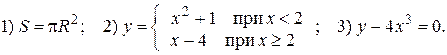
Аналитический способ задания функции является наиболее совершенным, так как к нему приложены методы математического анализа, позволяющие полностью исследовать функцию y = f (x).
Графический способ: задаётся график функции.
Часто графики вычерчиваются автоматически самопишущимися приборами или изображаются на экране дисплея. Значения функции у, соответствующие тем или иным значениям аргумента х, непосредственно находятся из этого графика.
Преимуществом графического способа задания функции является его наглядность, недостатком - его неточность.
Табличный способ: функция, задаётся таблицей ряда значений аргумента и соответствующих значений функции. Например, известные таблицы значений тригонометрических функций, логарифмические таблицы.
На практике часто приходится пользоваться таблицами значений функций, полученных опытным путём или в результате наблюдений.
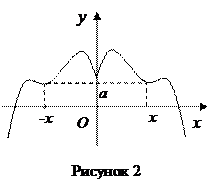 Основные свойства функций
Основные свойства функций
1. Функция y = f (x), определённая на множестве D, называется чётной, если 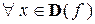 выполняется условие
выполняется условие 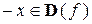 и
и
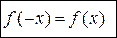 .
.
График чётной функции симметричен относительно оси Оу (рисунок 2).
Примеры чётных функций:
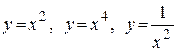 (рисунок 10),
(рисунок 10), 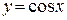 (рисунок 13).
(рисунок 13). 
2. 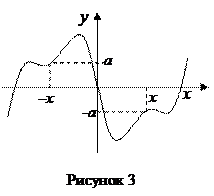 Функция y = f (x), определённая на множестве D, называется нечётной, если
Функция y = f (x), определённая на множестве D, называется нечётной, если 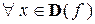 выполняется условие
выполняется условие 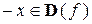 и
и
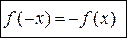 .
.
График нечётной функции симметричен относительно начала координат (рисунок 3).
Примеры нечётных функций:
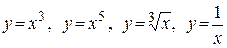 (рисунок 10),
(рисунок 10), 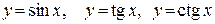 (рисунок 13)
(рисунок 13) 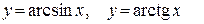 (рисунок 14).
(рисунок 14).
Область определения 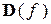 четной и нечетной функции симметричнаотносительно начала координат. Если это условие не выполнено, то функция не может быть ни четной, ни нечетной.
четной и нечетной функции симметричнаотносительно начала координат. Если это условие не выполнено, то функция не может быть ни четной, ни нечетной.
3. Функция  называетсяпериодической, если существует такое положительное число Т, что для
называетсяпериодической, если существует такое положительное число Т, что для 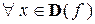 выполняется равенство
выполняется равенство

при этом число Т называют периодом функции.
Если Т – период функции  , то и пТ – также есть период этой функции, п Î Z. Число Т при этом называют основным или наименьшим периодом функции.
, то и пТ – также есть период этой функции, п Î Z. Число Т при этом называют основным или наименьшим периодом функции.
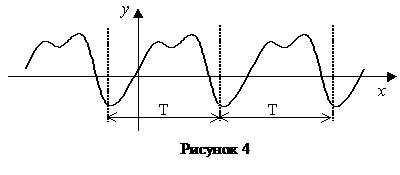 |
График периодической функции на любых двух соседних отрезках оси ОХ длины Т имеет один и тот же вид (рисунок 4).
Периодическими являются тригонометрические функции:
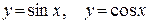 с периодом T = 2p;
с периодом T = 2p; 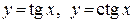 с периодом T = p.
с периодом T = p.
Для функций 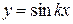 ,
,  период равен
период равен 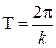 , а для
, а для 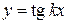 ,
, 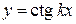 период равен
период равен 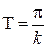 .
.
Если периодические функции  и
и 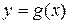 имеют соизмеримые периоды Т1 и Т2, т.е. такие, что пТ1 = тТ2, где п и т – некоторые целые числа, то они имеют общий период Т = пТ1 = тТ2.
имеют соизмеримые периоды Т1 и Т2, т.е. такие, что пТ1 = тТ2, где п и т – некоторые целые числа, то они имеют общий период Т = пТ1 = тТ2.
Если периодические функции  и
и 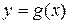 имеют один и тот же период Т, то функции
имеют один и тот же период Т, то функции 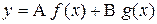 и
и 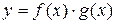 , где А и В – любые числа, также будут периодическими с периодом Т.
, где А и В – любые числа, также будут периодическими с периодом Т.
Если периоды функций  и
и 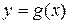 несоизмеримы, то функция
несоизмеримы, то функция 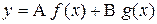 – не периодическая.
– не периодическая.
4. Функция  называется возрастающей на множестве
называется возрастающей на множестве 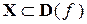 , если большему значению аргумента соответствует большее значение функции, т.е. для любых
, если большему значению аргумента соответствует большее значение функции, т.е. для любых 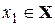 ,
,  , таких, что
, таких, что 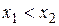 , выполняется неравенство
, выполняется неравенство 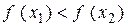 (рисунок 5, а).
(рисунок 5, а).
5. Функция  называется убывающей на множестве
называется убывающей на множестве 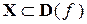 , если большему значению аргумента соответствует меньшее значение функции:
, если большему значению аргумента соответствует меньшее значение функции: 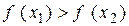 для любых
для любых 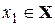 ,
,  ,
, 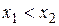 (рисунок 5, б).
(рисунок 5, б).
6.
 |
Функция
 называется ограниченнойна множестве
называется ограниченнойна множестве 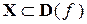 , если существуют такие числа А и В, что для всех
, если существуют такие числа А и В, что для всех 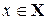 выполняется условие
выполняется условие
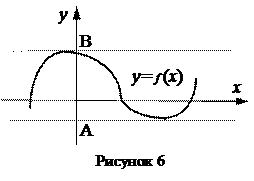
 .
.
Геометрически это означает, что график функции расположен в некоторой горизонтальной полосе между прямыми у = А и у = В. (рисунок 6)
Ограниченными в своей области определения являются функции 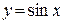 и
и 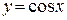 , т.к. для всех значений х выполняется
, т.к. для всех значений х выполняется 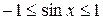 и
и 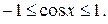
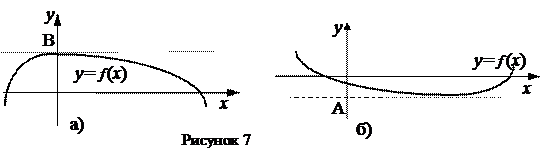 |
Если для всех значений
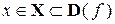 выполняется неравенство
выполняется неравенство 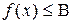 , то функция ограничена сверху на множестве Х (рисунок 7, а). Если же
, то функция ограничена сверху на множестве Х (рисунок 7, а). Если же  , то функция ограничена снизу (рисунок 7, б).
, то функция ограничена снизу (рисунок 7, б).
Примером ограниченной снизу функции служит показательная функция  т.к. для всех действительных значений х значения
т.к. для всех действительных значений х значения 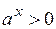 .
.
Обратная функция
 Пусть функция
Пусть функция  с областью определения D и множеством значенийE такова, что двум разным значениям аргумента ставит в соответствие разные числа, т.е. для любых
с областью определения D и множеством значенийE такова, что двум разным значениям аргумента ставит в соответствие разные числа, т.е. для любых 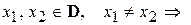
 Это означает, что функция принимает каждое своё значение у Î E только при одном значении аргумента хÎ D, т.е. функция
Это означает, что функция принимает каждое своё значение у Î E только при одном значении аргумента хÎ D, т.е. функция  задаёт между множествами Dи E взаимно однозначное соответствие.
задаёт между множествами Dи E взаимно однозначное соответствие.
Геометрически это отражается в том, что любая прямая, параллельная оси Ох, пересекает график функции  только один раз (рисунок 8).
только один раз (рисунок 8).
Определение. Если каждому значению у Î E поставить в соответствие число х такое, что  , то на множестве E будет определена функция, которая называется обратной для функции
, то на множестве E будет определена функция, которая называется обратной для функции  и обозначается
и обозначается 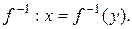 Функция
Функция  при этом называется обратимой, а функции f и
при этом называется обратимой, а функции f и 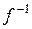 называются взаимно обратными.
называются взаимно обратными.
Чтобы найти функцию 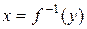 , обратную к функции
, обратную к функции  , достаточно решить уравнение
, достаточно решить уравнение 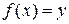 относительно х (если это возможно). Например, для функции у = 2х + 3 обратная функция определяется формулой
относительно х (если это возможно). Например, для функции у = 2х + 3 обратная функция определяется формулой 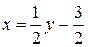 .
.
Из определения обратной функции вытекает следующая теорема.
Теорема 5.1.Если функция строго возрастает (убывает) на множестве D, то для неё существует обратная функция, которая также строго возрастает (убывает) на множестве значений Е исходной функции.
 Заметим, что функции
Заметим, что функции  и
и 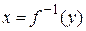 изображаются одной и той же кривой, т.е. их графики совпадают. Обычно, если функция f обратима, то и её аргумент, и аргумент обратной функции обозначают одной буквой х, т.е. записывают
изображаются одной и той же кривой, т.е. их графики совпадают. Обычно, если функция f обратима, то и её аргумент, и аргумент обратной функции обозначают одной буквой х, т.е. записывают  и
и 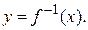 В рассматриваемом примере обратная к функции у = 2х + 3 есть функция
В рассматриваемом примере обратная к функции у = 2х + 3 есть функция 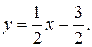
Другие примеры взаимно обратных функций: 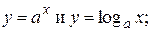
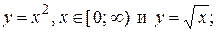
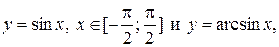 и т.д.
и т.д.
Взаимно обратные функции обладают свойствами:
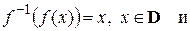
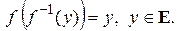
Область определения функции  совпадает с множеством значений функции
совпадает с множеством значений функции  множество значений функции
множество значений функции  совпадает с областью определения функции
совпадает с областью определения функции 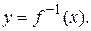 В символьных обозначениях это свойство выглядит так:
В символьных обозначениях это свойство выглядит так: 
Графики взаимно обратных функций  и
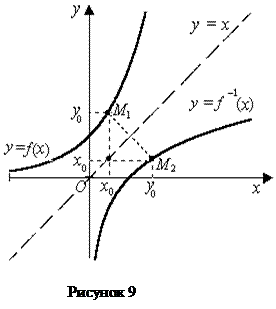
и  симметричны относительно биссектрисы первого и третьего координатных углов.
симметричны относительно биссектрисы первого и третьего координатных углов.
На рисунке 9 Точка 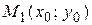
 становится точкой
становится точкой 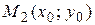 кривой
кривой 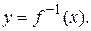 Но точки
Но точки 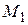 и
и  симметричны относительно прямой
симметричны относительно прямой 
Основные элементарные функции и их графики
Основными элементарными функциями называются следующие функции:
степенная 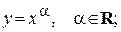
показательная 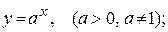
логарифмическая 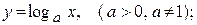
тригонометрические: 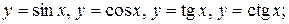
обратные тригонометрические:
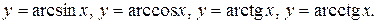
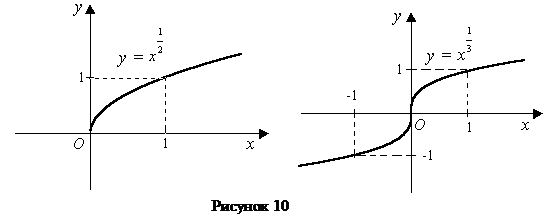
Степенная функция 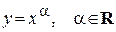 .
.
Примеры графиков степенных функций, соответствующих различным показателям степени, представлены на рисунке 10.
Для 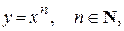 область определения —
область определения —  , а множество значений: при nчётном –
, а множество значений: при nчётном – 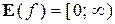 , при nнечётном
, при nнечётном 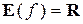 .
.
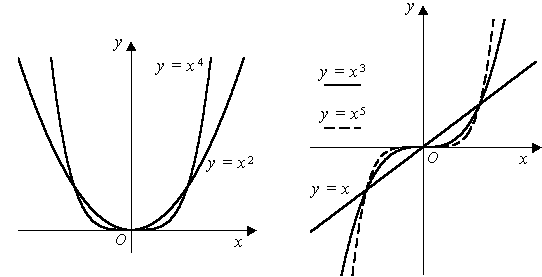
Для  область определения —
область определения — 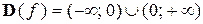 , а множество значений: при n чётном —
, а множество значений: при n чётном — 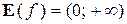 , при nнечётном —
, при nнечётном — 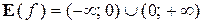
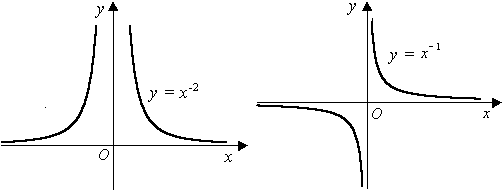
Для 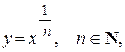 при nчётномобласть определения —
при nчётномобласть определения — 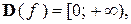 множество значений —
множество значений —  а при nнечётном область определения —
а при nнечётном область определения —  ,множество значений—
,множество значений— 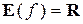 .
.
 |
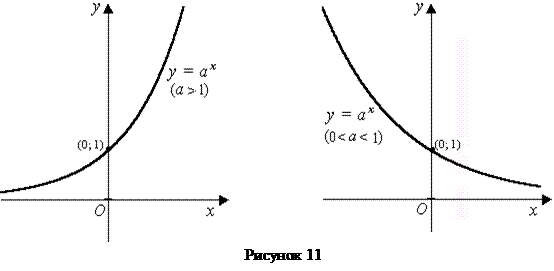
Показательная функция
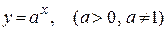 .
.
На рисунке 11 показаны графики показательных функций, соответствующие различным основаниям степени а:
 |
 ,
, 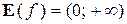 .
.
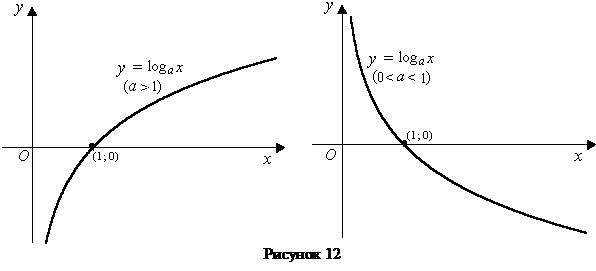
Логорифмическая функция 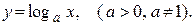
Графики логарифмических функций, соответствующие различным основаниям а, показаны на рисунке 12.
 |
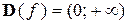 ,
, 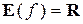 .
.
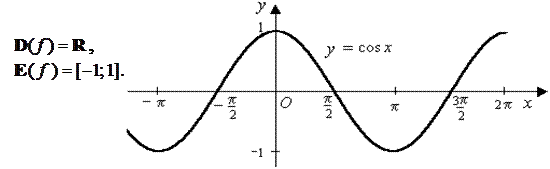
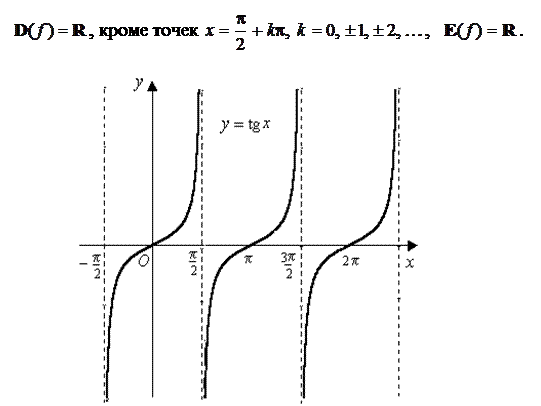
Тригонометрические функции: 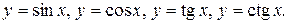
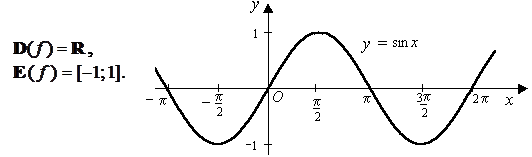 |
Графики этих функций имеют вид, показанный на рисунке 13.
 |
 |
 |
Обратные тригонометрические функции:
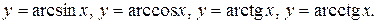 На рисунке 14 показаны графики обратных тригонометрических функций.
На рисунке 14 показаны графики обратных тригонометрических функций.

Функция, заданная одной формулой, составленной из основных элементарных функций и постоянных с помощью конечного числа арифметических операций (сложения, вычитания, умножения, деления) и операции взятия функции от функции, называется элементарной функцией.
Примерами элементарных функций могут служить функции
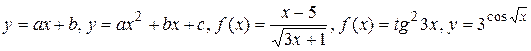 и т.п.
и т.п.
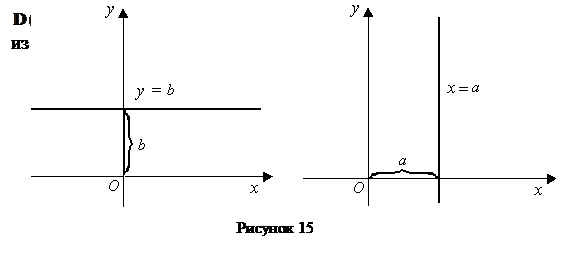
Линейная функция 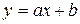 и её частные случаи
и её частные случаи 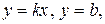
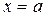
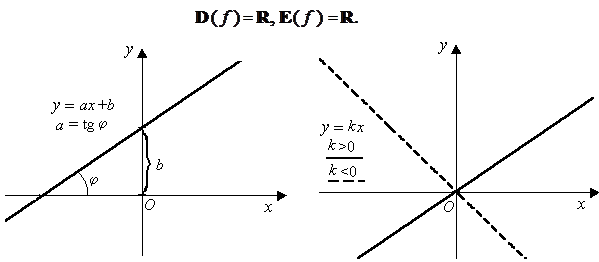
представлены на рисунке 15.
Квадратичная функфия  График функции - парабола с вершиной в точке с координатами
График функции - парабола с вершиной в точке с координатами 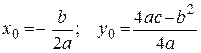 (рисунок 16).
(рисунок 16).
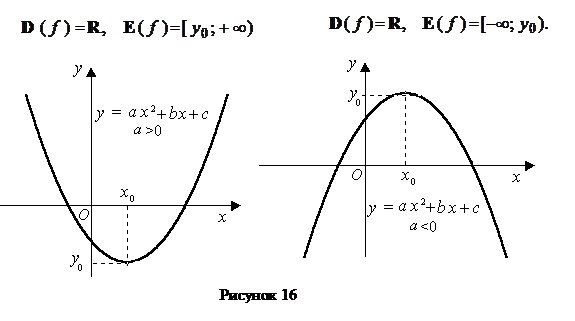 |
Примерами неэлементарныхфункций могут служить функции



Дата добавления: 2014-12-08; просмотров: 2766;
