Предел функции
Предел функции в точке и при 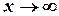
Предел функции — основной аппарат математического анализа. С его помощью определяется в дальнейшем непрерывность функции, производная, интеграл, сумма ряда.
Пусть функция y = f (x) определена в некоторой окрестности точки 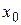 , кроме, быть может самой точки
, кроме, быть может самой точки 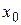 .
.
Сформулируем два, эквивалентных между собой, определения предела функции в точке.
Определение 1 (на «языке последовательностей», или по Гейне). Число b называется пределом функции y = f (x) в точке 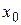 (или при
(или при  ), если для любой последовательности допустимых значений аргумента
), если для любой последовательности допустимых значений аргумента 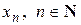
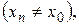 сходящейся к
сходящейся к 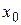 (т.е.
(т.е. 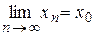 ), последовательность соответствующих значений функции
), последовательность соответствующих значений функции 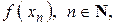 сходится к числу b (т.е.
сходится к числу b (т.е. 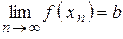 ).
).
В этом случае пишут  или
или 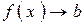 при
при  . Геометрический смысл предела функции:
. Геометрический смысл предела функции:  означает, что для всех точек х, достаточно близких к точке
означает, что для всех точек х, достаточно близких к точке 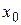 , соответствующие значения функции как угодно мало отличаются от числа b.
, соответствующие значения функции как угодно мало отличаются от числа b.
Определение 2 (на «языкеe-d», или по Коши). Число b называется пределом функции y = f (x) в точке 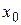 (или при
(или при  ), если для любого положительного числа e найдётся такое положительное число d, что для всех
), если для любого положительного числа e найдётся такое положительное число d, что для всех 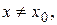 удовлетворяющих неравенству
удовлетворяющих неравенству 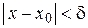 , выполняется неравенство
, выполняется неравенство 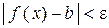 .
.
Записывают  .
.
Это определение коротко можно записать так:
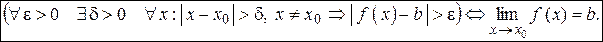
Заметим, что 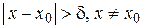 можно записать и так
можно записать и так 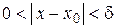 .
.
 Геометрический смысл предела функции:
Геометрический смысл предела функции:  , если для любой e-окрестности точки b найдётся такая d-окрестность точки
, если для любой e-окрестности точки b найдётся такая d-окрестность точки 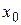 , что для всех
, что для всех  из этой d-окрестности соответствующие значения функции f (x) лежат в e-окрестности точки b. Иными словами, точки графика функции y = f (x) лежат внутри полосы шириной 2e, ограниченной прямыми у = b + e, у = b - e (рисунок 17). Очевидно, что величина d зависит от выбора e, поэтому пишут d = d(e).
из этой d-окрестности соответствующие значения функции f (x) лежат в e-окрестности точки b. Иными словами, точки графика функции y = f (x) лежат внутри полосы шириной 2e, ограниченной прямыми у = b + e, у = b - e (рисунок 17). Очевидно, что величина d зависит от выбора e, поэтому пишут d = d(e).
В определении предела функции  считается, что х стремится к
считается, что х стремится к 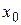 любым способом: оставаясь меньшим, чем
любым способом: оставаясь меньшим, чем 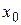 (слева от
(слева от 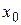 ), большим, чем
), большим, чем 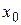 (справа от
(справа от 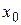 ), или колеблясь около точки
), или колеблясь около точки 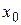 .
.
Бывают случаи, когда способ приближения аргумента х к 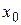 существенно влияет на значение предела функции. Поэтому вводят понятия односторонних пределов.
существенно влияет на значение предела функции. Поэтому вводят понятия односторонних пределов.
Определение. Число 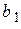 называется пределом функции y = f (x) слева в точке
называется пределом функции y = f (x) слева в точке 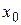 , если для любого числа e > 0 существует число d = d(e) > 0, такое, что при
, если для любого числа e > 0 существует число d = d(e) > 0, такое, что при 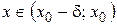 , выполняется неравенство
, выполняется неравенство 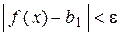 .
.
Предел слева записывается так 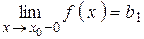 или коротко
или коротко  (обозначение Дирихле) (рисунок 18).
(обозначение Дирихле) (рисунок 18).
Аналогично определяется предел функции справа, запишем его с помощью символов:
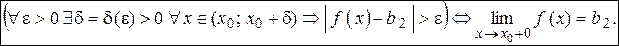 Коротко предел справа обозначается
Коротко предел справа обозначается  .
.
 Пределы функции слева и справа называются односторонними пределами. Очевидно, если существует
Пределы функции слева и справа называются односторонними пределами. Очевидно, если существует  , то существуют оба односторонних предела, причём
, то существуют оба односторонних предела, причём 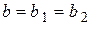 .
.
Справедливо и обратное утверждение: если существуют оба предела  и
и 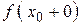 и они равны, то существует предел
и они равны, то существует предел  и
и 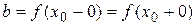 .
.
Если же 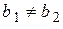 , то
, то 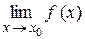 не существует.
не существует.
Определение. Пусть функция y = f (x) определена в промежутке  . Число b называется пределом функции y = f (x) при х ® ¥, если для любого числа e > 0 существует такое число М = М (e) > 0, что при всех х, удовлетворяющих неравенству
. Число b называется пределом функции y = f (x) при х ® ¥, если для любого числа e > 0 существует такое число М = М (e) > 0, что при всех х, удовлетворяющих неравенству 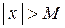 выполняется неравенство
выполняется неравенство 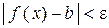 . Коротко это определение можно записать так:
. Коротко это определение можно записать так:
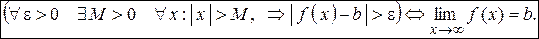
 Если х ® +¥, то пишут
Если х ® +¥, то пишут 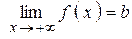 , если х ® -¥, то пишут
, если х ® -¥, то пишут 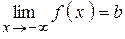 , если
, если 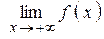 =
= 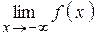 , то их общее значение принято обозначать
, то их общее значение принято обозначать 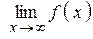 .
.
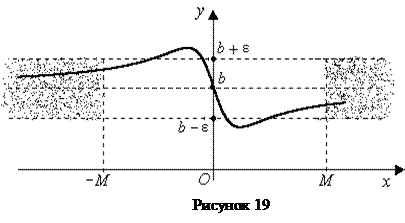
Геометрический смысл этого определения таков: для 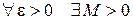 , что при
, что при 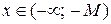 и
и  соответствующие значения функции y = f (x) попадают в e-окрестность точки b, т.е. точки графика лежат в полосе шириной 2e, ограниченной прямыми
соответствующие значения функции y = f (x) попадают в e-окрестность точки b, т.е. точки графика лежат в полосе шириной 2e, ограниченной прямыми 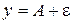 и
и  (рисунок 19).
(рисунок 19).
Бесконечно большие функции (б.б.ф)
Бесконечно малые функции (б.м.ф)
Определение. Функция y = f (x) называется бесконечно большой при  , если для любого числа М > 0 существует число d = d(М) > 0, что для всех х, удовлетворяющих неравенству
, если для любого числа М > 0 существует число d = d(М) > 0, что для всех х, удовлетворяющих неравенству 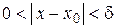 , выполняется неравенство
, выполняется неравенство  Записывается
Записывается  или
или  при
при  .
.
Коротко:
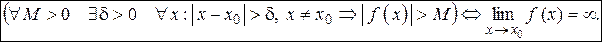
Например, функция 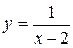 есть б.б.ф. при
есть б.б.ф. при  .
.
Если f (x) стремится к бесконечности при  и принимает лишь положительные значения, то пишут
и принимает лишь положительные значения, то пишут 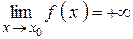 ; если лишь отрицательные значения, то
; если лишь отрицательные значения, то 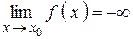 .
.
Определение. Функция y = f (x), заданная на всей числовой оси, называется бесконечно большой при 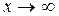 , если для любого числа М > 0 найдётся такое число N = N (М) > 0, что для всех х, удовлетворяющих неравенству
, если для любого числа М > 0 найдётся такое число N = N (М) > 0, что для всех х, удовлетворяющих неравенству  , выполняется неравенство
, выполняется неравенство  Записывается
Записывается 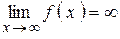 . Коротко:
. Коротко:

Например, 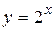 есть б.б.ф. при
есть б.б.ф. при 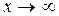 .
.
Отметим, что если аргумент х, стремясь к бесконечности, принимает лишь натуральные значения, т.е.  , то соответствующая б.б.ф. становится бесконечно большой последовательностью. Например, последовательность
, то соответствующая б.б.ф. становится бесконечно большой последовательностью. Например, последовательность  является бесконечно большой последовательностью. Очевидно, всякая б.б.ф. в окрестности точки
является бесконечно большой последовательностью. Очевидно, всякая б.б.ф. в окрестности точки 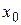 является неограниченной в этой окрестности. Обратное утверждение неверно: неограниченная функция может не быть б.б.ф. (Например,
является неограниченной в этой окрестности. Обратное утверждение неверно: неограниченная функция может не быть б.б.ф. (Например, 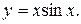 )
)
Однако, если  , где b - конечное число, то функция f (x ограничена в окрестности точки
, где b - конечное число, то функция f (x ограничена в окрестности точки 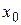 .
.
Действительно, из определения предела функции следует, что при  выполняется условие
выполняется условие 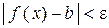 . Следовательно,
. Следовательно, 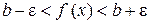 при
при 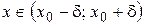 , а эот означает, что функция f (x) ограничена.
, а эот означает, что функция f (x) ограничена.
Определение. Функция y = f (x) называется бесконечно малой при  , если
, если
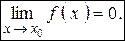
По определению предела функции это равенство означает: для любого числа 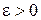 найдётся число
найдётся число 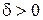 такое, что для всех х, удовлетворяющих неравенству
такое, что для всех х, удовлетворяющих неравенству 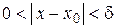 , выполняется неравенство
, выполняется неравенство 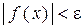 .
.
Аналогично определяется б.м.ф. при 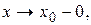
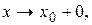
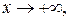
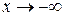 : Во всех этих случаях
: Во всех этих случаях 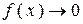 .
.
Бесконечно малые функции часто называют бесконечно малыми величинами или бесконечно малыми; обозначаются обычно греческими буквами a, b и т.д.
Примерами б.м.ф. служат функции 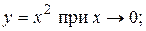
 при
при 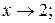
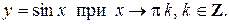
Другой пример: 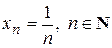 - бесконечно малая последовательность.
- бесконечно малая последовательность.
Пример Доказать, что 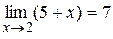 .
.
Решение. Функцию 5 + х можно представить в виде суммы числа 7 и б.м.ф. х - 2 (при 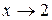 ), т.е. выполнено равенство
), т.е. выполнено равенство  . Следовательно, по теореме 3.4.6 получаем
. Следовательно, по теореме 3.4.6 получаем 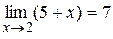 .
.
Основные теоремы о пределах
Рассмотрим теоремы (без доказательства), которые облегчают нахождение пределов функции. Формулировка теорем для случаев, когда 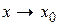 и
и 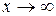 , аналогично. В приводимых теоремах будем считать, что пределы
, аналогично. В приводимых теоремах будем считать, что пределы 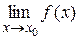 ,
, 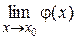 существуют.
существуют.
Теорема 5.8Предел суммы (разности) двух функций равен сумме (разности) их пределов: 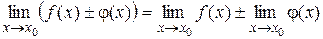 .
.
Теорема 5.9 Предел произведения двух функций равен произведению их пределов: 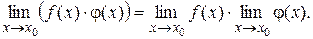
Отметим, что теорема справедлива для произведения любого конечного числа функций.
Следствие 3 Постоянный множитель можно выносить за знак предела: 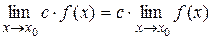 .
.
Следствие 4 Предел степени с натуральным показателем равен той же степени предела:  . В частности,
. В частности, 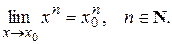
Теорема 5.10 Предел дроби равен пределу числителя, делённому на предел знаменателя, если предел знаменателя не равен нулю:
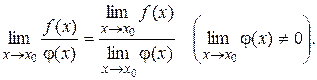
ПримерВычислить 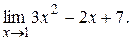
Решение. 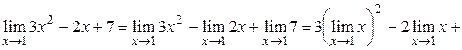
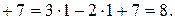
ПримерВычислить 
Решение. Здесь применить теорему о пределе дроби нельзя, т.к. предел знаменателя, при 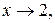 равен 0. Кроме того, предел числителя равен 0. В таких случаях говорят, что имеем неопределённость вида
равен 0. Кроме того, предел числителя равен 0. В таких случаях говорят, что имеем неопределённость вида 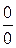 . Для её раскрытия разложим числитель и знаменатель дроби на множители, затем сократим на
. Для её раскрытия разложим числитель и знаменатель дроби на множители, затем сократим на 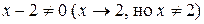 :
:
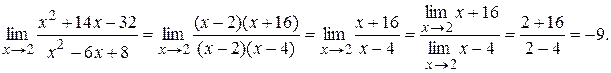
ПримерВычислить 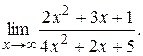
Решение. Здесь мы имеем дело с неопределённость вида 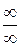 . Для нахождения предела данной дроби разделим числитель и знаменатель на
. Для нахождения предела данной дроби разделим числитель и знаменатель на 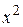 :
:
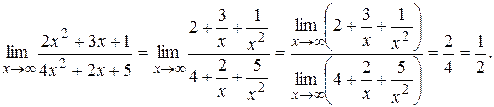
Функция 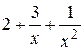 есть сумма числа 2 и б.м.ф., поэтому
есть сумма числа 2 и б.м.ф., поэтому

Признаки существования пределов
Не всякая функция, даже ограниченная, имеет предел. Например, функция 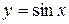 при
при 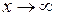 предела не имеет. Во многих вопросах анализа бывает достаточно только убедится в существовании предела функции. В таких случаях пользуются признаками существования предела.
предела не имеет. Во многих вопросах анализа бывает достаточно только убедится в существовании предела функции. В таких случаях пользуются признаками существования предела.
Первый и второй замечательные пределы
Определение. При вычислении пределов выражений, содержащих тригонометрические функции, часто используют предел
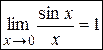 ,
,
называемый первым замечательным пределом.
Читается: предел отношения синуса к его аргументу равен единице, когда аргумент стремится к нулю.
Пример Найти 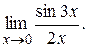
Решение. Имеем неопределённость вида 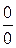 . Теорема о пределе дроби неприменима. Обозначим
. Теорема о пределе дроби неприменима. Обозначим 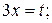 тогда при
тогда при 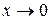 и
и 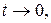
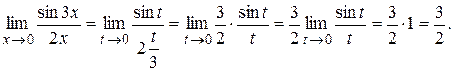
Пример 3 Найти 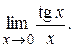
Решение. 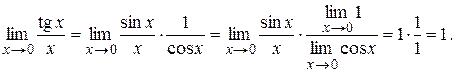
Определение.Равенства 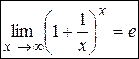 и
и 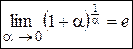 называются вторым замечательным пределом.
называются вторым замечательным пределом.
Замечание. Известно, что предел числовой последовательности
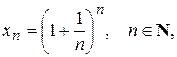 имеет предел, равный е :
имеет предел, равный е : 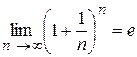 . Число е называют неперовым числом. Число е иррациональное, его приближённое значение равно 2,72 (е = 2, 718281828459045…). Некоторые свойства числа е делают особенно удобным выбор этого числа в качестве основания логарифмов. Логарифмы по основанию е называются натуральными логарифмами и обозначаются
. Число е называют неперовым числом. Число е иррациональное, его приближённое значение равно 2,72 (е = 2, 718281828459045…). Некоторые свойства числа е делают особенно удобным выбор этого числа в качестве основания логарифмов. Логарифмы по основанию е называются натуральными логарифмами и обозначаются 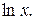 Заметим, что
Заметим, что
 .
.
Примем без доказательства утверждение, что к числу е стремится и функция 
Если положить 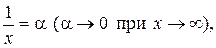 то из
то из 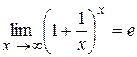 следует
следует 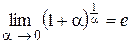 . Эти равенства широко используются при вычислении пределов. В приложениях анализа большую роль играет показательная функция с основанием е. Функция
. Эти равенства широко используются при вычислении пределов. В приложениях анализа большую роль играет показательная функция с основанием е. Функция 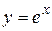 называется экспоненциальной, употребляется также обозначение
называется экспоненциальной, употребляется также обозначение 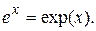
Пример Найти 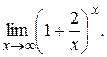
Решение. Обозначим 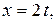 очевидно,
очевидно, 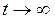 при
при 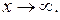 Имеем
Имеем
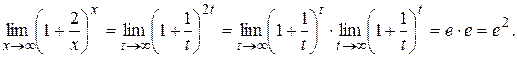
Вычисление пределов
Для раскрытия неопределённостей вида 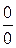 часто бывает полезным применять принцип замены бесконечно малых эквивалентными и другие свойства эквивалентных бесконечно малых функций. Как известно,
часто бывает полезным применять принцип замены бесконечно малых эквивалентными и другие свойства эквивалентных бесконечно малых функций. Как известно,  ~ x при
~ x при 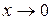 т.к.
т.к. 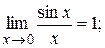
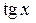 ~ x при
~ x при 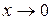 , т.к.
, т.к. 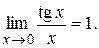
Пример Покажем, что 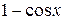 ~
~  при
при 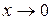 .
.
Решение. 
ПримерНайдём 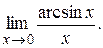
Решение. Обозначим 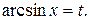 Тогда
Тогда 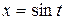 и
и 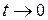 при
при 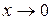 . Поэтому
. Поэтому
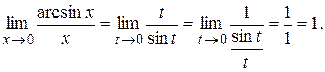
Следовательно, 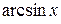 ~ x при
~ x при 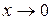 .
.
Пример Покажем, что 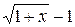 ~
~ 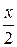 при
при 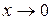 .
.
Решение. Так как
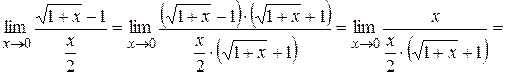
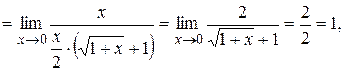
то 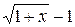 ~
~ 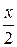 при
при 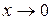 .
.
Ниже приведены важнейшие эквивалентности, которые используются при вычислении пределов.
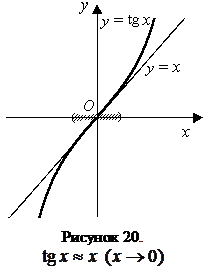
1.  ~ x при ~ x при 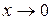 ; ;
| 6. 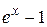 ~ x ( ~ x ( 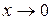 ); );
|
2. 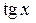 ~ x ( ~ x ( 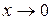 ); );
| 7. 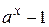 ~ ~ 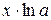 ( ( 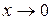 ); );
|
3. 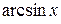 ~ x ( ~ x ( 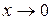 ); );
| 8. 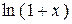 ~ x ( ~ x ( 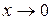 ); );
|
4. 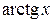 ~ x ( ~ x ( 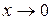 ); );
| 9. 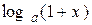 ~ ~ 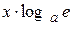 ( ( 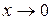 ); );
|
5. 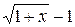 ~ ~ 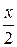 ( ( 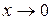 ); );
| 10. 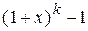 ~ ~ 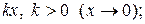 в частности
в частности 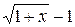 ~ ~ 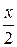 ( ( 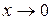 ). ).
|
Пример Найти 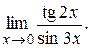
Решение. Так как 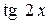 ~ 2x,
~ 2x, 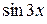 ~ 3x при
~ 3x при 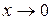 , то
, то

Пример Найти 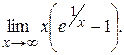
Решение. Обозначим  , из
, из 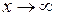 следует
следует 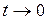 . Поэтому
. Поэтому
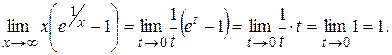
Пример Найти 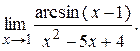
Решение. Так как  ~ (x - 1) при
~ (x - 1) при  , то
, то
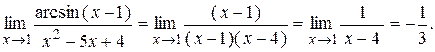
Пример Найти приближённое значение для 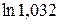 .
.
Решение. 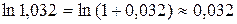 . Для сравнения результата по таблице логарифмов находим, что
. Для сравнения результата по таблице логарифмов находим, что 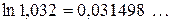 .
.
Дата добавления: 2014-12-08; просмотров: 4733;
