Классификация точек разрыва
Определение. Точки, в которых нарушается непрерывность функции, называются точками разрыва этой функции.
Если 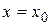 — точка разрыва функции
— точка разрыва функции  , то в ней не выполняется по крайней мере одно из условий первого определения непрерывности функции, а именно:
, то в ней не выполняется по крайней мере одно из условий первого определения непрерывности функции, а именно:
· Функция определена в окрестности точки  , но не определена в самой точке
, но не определена в самой точке  . Например, функция
. Например, функция 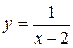 не определена в точке
не определена в точке 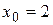 (рисунок 26).
(рисунок 26).
·
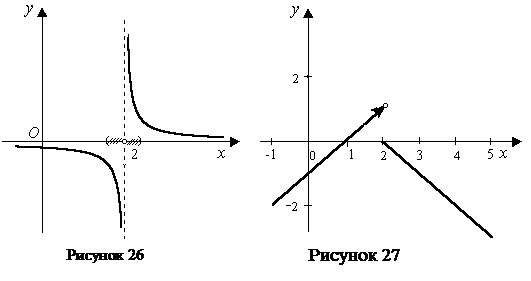 |
Функция определена в точке
 и её окрестности, но не существует предела
и её окрестности, но не существует предела 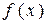 при
при  .
.
Например, функция
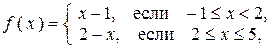 определена в точке
определена в точке 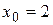 ( f (2) = 0), однако в точке
( f (2) = 0), однако в точке 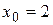 имеет разрыв (рисунок 27), т.к. эта функция не имеет предела при
имеет разрыв (рисунок 27), т.к. эта функция не имеет предела при 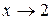 :
:
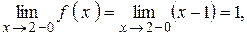
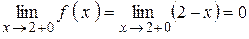 .
.
· Функция определена в точке  и её окрестности существует
и её окрестности существует 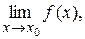 но этот предел не равен значению функции в точке
но этот предел не равен значению функции в точке  :
: 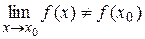 .
.
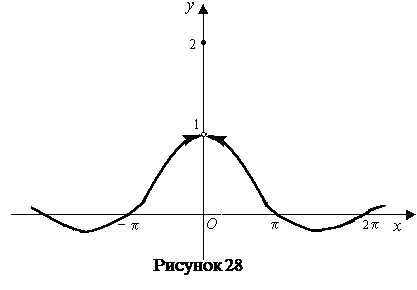
Например, функция 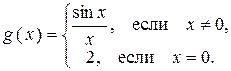 (рисунок 28). Здесь
(рисунок 28). Здесь 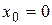 – точка разрыва, т.к
– точка разрыва, т.к 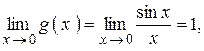 а
а 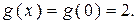
 |
Все точки разрыва функции разделяются на точки разрыва первого и второго рода.
Определение.Точка разрыва  называется точкой разрыва первого рода функции
называется точкой разрыва первого рода функции  , если в этой точке существуют конечные пределы функции слева и справа (односторонние пределы), т. е.
, если в этой точке существуют конечные пределы функции слева и справа (односторонние пределы), т. е. 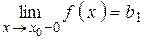 и
и 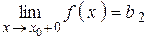 . При этом:
. При этом:
а) если 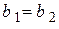 , то точка
, то точка  называется точкой устранимого разрыва;
называется точкой устранимого разрыва;
б) если 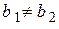 , то точка
, то точка  называется точкой конечного разрыва. Величину
называется точкой конечного разрыва. Величину 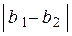 называют скачком функции в точке разрыва первого рода.
называют скачком функции в точке разрыва первого рода.
Точка разрыва  называется точкой разрыва второго рода функции
называется точкой разрыва второго рода функции  , если по крайней мере один из односторонних пределов (слева, или справа, или оба вместе) не существует или равен бесконечности.
, если по крайней мере один из односторонних пределов (слева, или справа, или оба вместе) не существует или равен бесконечности.
Обратимся к функциям, рассмотренным выше.
Для функции 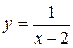 ,
, 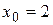 — точка разрыва второго рода (рисунок 26).
— точка разрыва второго рода (рисунок 26).
Для функции 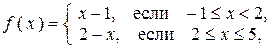
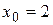 является точкой разрыва первого рода (рисунок 27), скачок функции равен
является точкой разрыва первого рода (рисунок 27), скачок функции равен 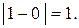
Для функции 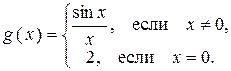
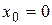 является точкой устранимого разрыва первого рода (рисунок 28). Положив
является точкой устранимого разрыва первого рода (рисунок 28). Положив 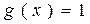 (вместо
(вместо 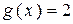 ) при
) при 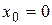 , разрыв устранится, функция станет непрерывной.
, разрыв устранится, функция станет непрерывной.
Пример Дана функция 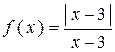 . Найти точки разрыва, выяснить их тип.
. Найти точки разрыва, выяснить их тип.
Решение. Функция 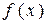 определена и непрерывна на всей числовой оси, кроме точки
определена и непрерывна на всей числовой оси, кроме точки 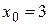 . Очевидно,
. Очевидно, 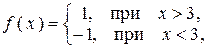
Следовательно, 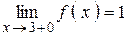 , а
, а 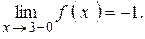 Поэтому в точке
Поэтому в точке 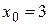 функция имеет разрыв первого рода. Скачок функции в этой точке равен
функция имеет разрыв первого рода. Скачок функции в этой точке равен 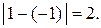
Дата добавления: 2014-12-08; просмотров: 1784;
