Непрерывность элементарных функций
Теоремы о непрерывности функций следуют непосредственно из соответствующих теорем о пределах. Приведем их тоже без доказательства
Теорема 5.16 Сумма, произведение и частное двух непрерывных функций есть функция непрерывная (для частного за исключением тех значений аргумента, в которых делитель равен нулю).
Теорема 5.17 Пусть функция 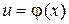 непрерывна в точке
непрерывна в точке  , а функция
, а функция 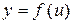 непрерывна в точке
непрерывна в точке 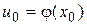 . Тогда сложная функция
. Тогда сложная функция 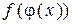 , состоящая из непрерывных функций, непрерывна в точке
, состоящая из непрерывных функций, непрерывна в точке  .
.
Теорема 5.18 Если функция  непрерывна и строго монотонна на
непрерывна и строго монотонна на 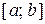 оси Ох, то обратная функция
оси Ох, то обратная функция  также непрерывна и монотонна на соответствующем отрезке
также непрерывна и монотонна на соответствующем отрезке  оси Оу .
оси Оу .
Например, функция 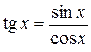 , в силу теоремы 3.16, есть функция непрерывная для всех значений х, кроме тех, для которых
, в силу теоремы 3.16, есть функция непрерывная для всех значений х, кроме тех, для которых 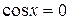 , т.е. кроме значений
, т.е. кроме значений 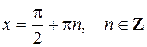 . Функции
. Функции 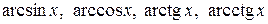 , в силу теоремы 3.18, непрерывны при всех значений х при которых эти функции определены.
, в силу теоремы 3.18, непрерывны при всех значений х при которых эти функции определены.
Теорема 5.19 Все основные элементарные функции непрерывны при всех значениях х, для которых они определены.
Как известно, элементарнойназывается такая функция, которую можно задать одной формулой, содержащей конечное число арифметических действий и суперпозиций (операции взятия функции от функции) основных элементарных функций. Поэтому из приведённых выше теорем вытекает:
Теорема 5.20 Всякая элементарная функция непрерывна в каждой точке, в которой она определена.
Этот важный результат позволяет, в частности, легко находить пределы элементарных функций в точках, где они определены.
Пример Найти 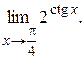
Решение. Функция 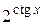 непрерывна в точке
непрерывна в точке 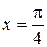 , поэтому
, поэтому 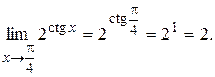
Дата добавления: 2014-12-08; просмотров: 1422;
