И построению ее графика

Методы дифференциального исчисления позволяют исследовать функции и строить их графики. Так, по знаку первой производной в интервале можно определить возрастание (убывание) функции, делать выводы о наличии или отсутствии экстремума функции. По знаку второй производной выделяем интервалы выпуклости (вогнутости) графика функции и точки перегиба ее графика.

Справедливы следующие теоремы:

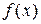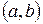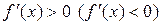1. Если функция дифференцируема на интервале и для 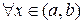, то эта функция возрастает (убывает) на интервале .

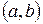2. Если дифференцируемая функция 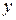= 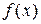имеет экстремум в точке х 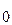, то ее производная в этой точке равна нулю: .

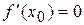3. Если непрерывная функция 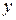= 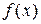дифференцируема в некоторой 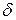-окрестности критической точки х 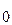и при переходе через нее (слева направо) производная 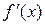меняет знак с плюса на минус, то х 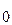- точка максимума; с минуса на плюс, то х 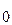- точка минимума.

4. Если функция 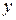= 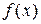во всех точках интервала 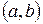имеет отрицательную вторую производную, то график функции в этом интервале выпуклый верх; если 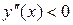, то график выпуклый вниз.

5. Если вторая производная 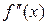при переходе через точку х 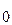, в которой она равна нулю или не существует, меняет знак, то точка графика с абсциссой х 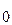- точка перегиба.

Построение графика функции значительно облегчается, если известны его асимптоты.

Различают 2 вида асимптот:

а) Вертикальные, существующие в точках разрыва второго рода. Их уравнения имеют вид .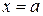

б) Наклонны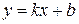е: , где

, .

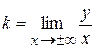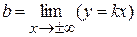В частности, при 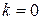наклонная асимптота становится горизонтальной и имеет уравнение .

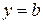При исследовании функции и построении ее графика полезно воспользоваться следующей схемой:

1. Найти область определения функции.

2. Найти точки пересечения графика с осями координат, если это возможно.

3. Найти асимптоты графика функции.

4. Найти интервалы монотонности и точки экстремума функции.

5. Найти интервалы выпуклости и вогнутости и точки перегиба графика функции.

На основании полученного исследования построить график.

Пример 7 Исследовать функцию и построить ее график:

.

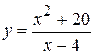Решение.

1. Область определения.

.

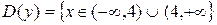2. Асимптоты графика:

а) вертикальная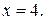

б) наклонная 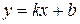, где

.

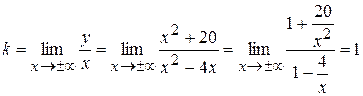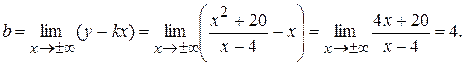
3. Найдем производную функции.

; ; .

.

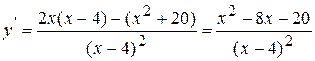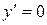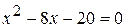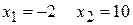Определим знак производной в промежутках:

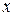
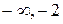	( )	-2	-2, 4		(4, 10)		(10, + )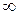
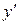
	+		-	не сущ.			+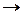
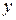
		max				min

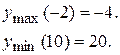
4. Найдем вторую производную функции.

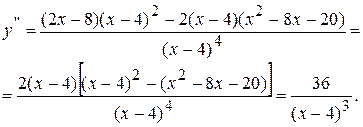
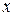
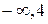	( )		(4, + )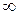
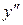
	-	не сущ.	+

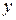
Точек перегиба графика функции нет.

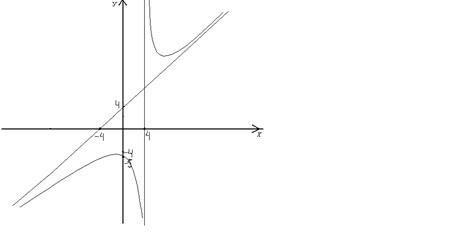По результатам исследования построим график функции.

Вопросы для самопроверки

1. Каковы признаки возрастания и убывания функции?

2. Что называется экстремумом функции?

3. Сформулируйте необходимые и достаточные признаки существования экстремума функции.

4. Как найти интервалы выпуклости и вогнутости кривой и точки перегиба графика функции?

5. Что называется асимптотой кривой?

6. Каких видов бывают асимптоты графика функции и как их найти?