Производная функции
Понятие производной функции является одним из основных в математике и широко применяется в различных областях науки и техники.
Производной функции y=f(x) в точке х 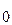 называется предел отношения приращения функции к приращению аргумента, когда последнее стремится к нулю произвольным образом.
называется предел отношения приращения функции к приращению аргумента, когда последнее стремится к нулю произвольным образом.
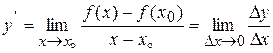 .
.
Процедура отыскания производной называется дифференцированием функции.
Справедливы следующие правила дифференцирования:
1. (с)  =0 2. (u+v)
=0 2. (u+v)  =u
=u  +v
+v  3. (uv)
3. (uv)  =u
=u  v+uv
v+uv 
4. (сu)  = сu
= сu  5.
5. 
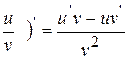 .
.
На основе этого определения могут быть выведены формулы для производных основных элементарных функций:
1. 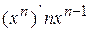 , в частности:
, в частности: 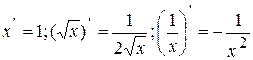 ;
;
2. 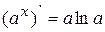 , в частности:
, в частности: 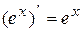 ;
;
3.  , в частности:
, в частности: 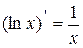 ;
;
4. 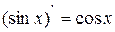 ; 5.
; 5.  ;
;
6. 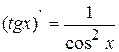 ; 7.
; 7. 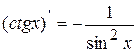 ;
;
8.  ; 9.
; 9.  ;
;
10. 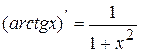 ; 11.
; 11. 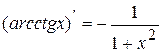 .
.
Особый интерес представляет производная сложной функции.
Если у=f(u), где u= 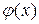 , тогда у
, тогда у 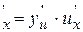 .
.
Пример 1 Найти производную функции: 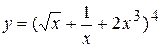 .
.
Решение.
Используя правило дифференцирования сложной функции, а также формулу нахождения производной степенной функции, получим:
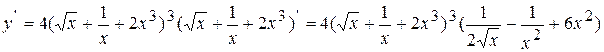 .
.
Пример 2 Найти производную функции 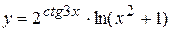 .
.
Решение.
Воспользуемся правилом дифференцирования произведения двух функций и формулами нахождения производной от показательной и логарифмической функции.
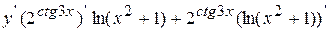 = =
= = 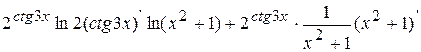 = =
= = 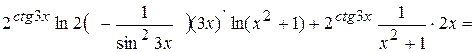
= 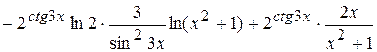 .
.
Пример 3 Найти производную функции: 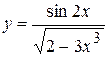 .
.
Используем правило дифференцирования дроби и формулы нахождения производной от 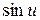 и степенной функции.
и степенной функции.
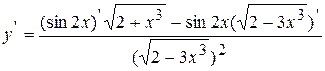 =
=
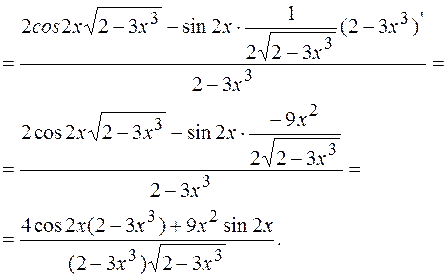
Пример 4 Найти производную функции:  .
.
Решение.
При нахождении производной неявно заданной функции продифференцируем обе части уравнения по переменной 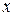 , имея в виду, что
, имея в виду, что 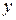 есть функция от
есть функция от 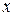 и выразим
и выразим 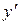 из полученного линейного относительно
из полученного линейного относительно 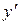 уравнения.
уравнения.
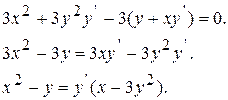
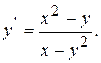
Если функция задана параметрическими уравнениями, то ее производная по переменной 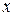 находится по формуле
находится по формуле 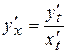 .
.
Пример 5 Найти производную функции: 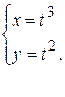
Решение.
Поскольку  ,
, 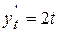 , то
, то
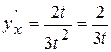 .
.
Пример 6 Найти производную функции: 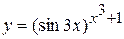 .
.
Решение.
Применим метод логарифмического дифференцирования, для чего логарифмируем заданное выражение по основанию «  », потом дифференцируем и находим у
», потом дифференцируем и находим у  .
.
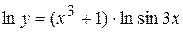 .
.
Дифференцируем:
 =
=
= 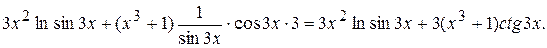
Находим из полученного уравнения у  :
:
 .
.
Вопросы для самопроверки
1. Что называется производной функции?
2. Каковы правила нахождения производных от суммы, произведения, дроби, от постоянной величины?
3. Как найти производную сложной функции?
4. Правило дифференцирования функции, заданной неявно.
5. В чем заключается метод логарифмического дифференцирования?
Дата добавления: 2014-12-08; просмотров: 1089;
