Асимптоты графика функции. Для окончательной ВТО мужских брюк типа джинсов, где не нужны складки, стрелки

Для окончательной ВТО мужских брюк типа джинсов, где не нужны складки, стрелки. Изделие зажимают сверху и снизу, и в него подается пар и горячий воздух, затем холодный воздух для просушивания. Эффект аналогичен ПВМ (Формфинишер серия 600 V).
Отпаривание –декатировочный процесс для снятия остаточных напряжений с целью устранения усадки ткани при последующей эксплуатации. Применяется редко, так как при отпаривании осуществляется воздействие на волокна, расположенные по всей толщине материала, а не только на ее поверхности, вследствие чего устраняется эффект, полученный в предшествующей ВТО. Сейчас вновь актуально для шерстяных и проблемных тканей.
Отпаривание может производиться паровой щеткой Veit 2157 – для разравнивания ткани, освежения внешнего вида, избавления от складок, глянца и отпечатков на ткани. Для окончательной ВТО после формования. Отпариватель имеет форму утюга с большим количеством отверстий в подошве, с подводимым через шланг паром; с тефлоновой подошвой.
Для отпаривания кожи и чувствительных материалов используется насадка. Пар используется либо сухой, либо насыщенный в зависимости от потребности.
Кроме того, может использоваться держатель с подставкой, который перемещает щетку в желаемую позицию и вместе с этим обеспечивает возможность работать, не уставая.
Фиксация швейных изделий применяется преимущественно для трикотажных изделий с целью стабилизации текстильных волокон. Конструкция машин аналогична раннее рассмотренным, но время воздействия подушек меньше, чем для ткани.
Асимптоты графика функции
● Прямая 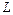 называется асимптотой графика функции
называется асимптотой графика функции 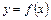 , если расстояние от некоторой точки
, если расстояние от некоторой точки 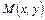 , лежащей на графике, до этой прямой
, лежащей на графике, до этой прямой 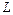 стремится к нулю при стремлении хотя бы одной из координат точки
стремится к нулю при стремлении хотя бы одной из координат точки 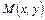 к бесконечности.
к бесконечности.
Существуют два вида асимптот: вертикальные и наклонные.
● Прямая 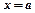 называется вертикальной асимптотой графика функции
называется вертикальной асимптотой графика функции 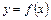 , если
, если
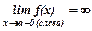 или или 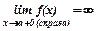 . .
| (4.3.1) |
Вертикальных асимптоты ищутся среди точек разрыва.
Пример 4.3.1. Найти вертикальные асимптоты графиков функций:
1) 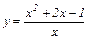
| 2) 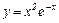
|
Решение.
1) Вертикальные асимптоты ищутся среди точек разрыва, т. е. в нашем случае рассмотрим 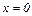 .
.
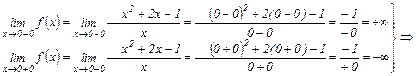
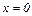 – вертикальная асимптота.
– вертикальная асимптота.
2) Очевидно, вертикальных асимптот нет, т. к. нет точек разрыва.
● Прямая 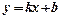 называется наклонной асимптотой графика функции
называется наклонной асимптотой графика функции 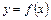 , если существуют конечные пределы:
, если существуют конечные пределы:
левая наклонная асимптота
при 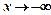
| правая наклонная асимптота
при 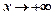
| (4.3.2) |
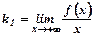 , , 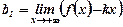 , ,
| 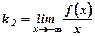 , , 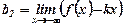 . .
|
Замечание. В некоторых случаях функция асимптотически приближается к одной и той же прямой при 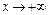 и
и 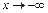 , тогда наклонная асимптота будет одна при
, тогда наклонная асимптота будет одна при 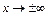 .
.
● При 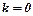 прямая
прямая 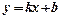 примет вид
примет вид 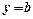 и наклонная асимптота будет горизонтальной.
и наклонная асимптота будет горизонтальной.
Пример 4.3.2. Найти наклонные асимптоты графиков функций
1) 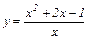
| 2) 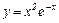
|
Решение.
1) 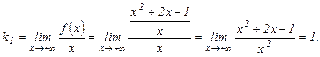
Соответственно,
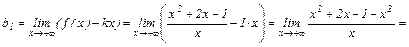
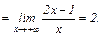
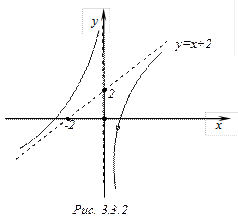
Таким образом, имеется правая (при 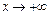 ) наклонная асимптота
) наклонная асимптота 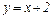 . Аналогично можно показать, что эта же прямая является наклонной асимптотой и при
. Аналогично можно показать, что эта же прямая является наклонной асимптотой и при 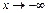 .
.
Таким образом, при 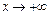 так и при
так и при 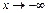 функция асимптотически приближается к одной и той же прямой
функция асимптотически приближается к одной и той же прямой 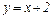 (рис. 4.3.1).
(рис. 4.3.1).
|
2) 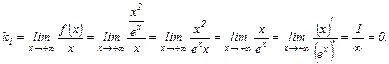
Соответственно, 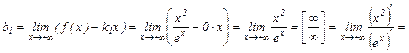
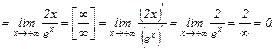
Таким образом, имеется правая (при 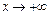 ), т. к.
), т. к. 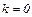 горизонтальная асимптота
горизонтальная асимптота 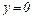 .
.
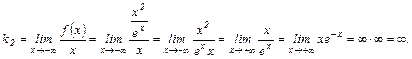 Следовательно, при
Следовательно, при 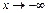 асимптот не будет ( рис. 4.3.2).
асимптот не будет ( рис. 4.3.2).
|
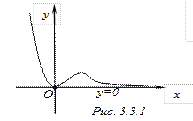
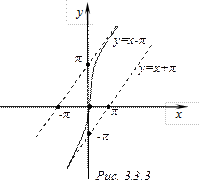
Пример 4.3.3. Найти асимптоты графиков функций
1) 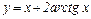
| 2) 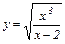
|
Решение.
1) Очевидно, вертикальных асимптот нет, т. к. нет точек разрыва.
Исследуем поведение функции при 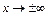 , т. е. найдём наклонные (горизонтальные) асимптоты
, т. е. найдём наклонные (горизонтальные) асимптоты 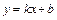 .
.
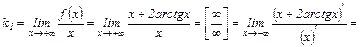
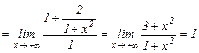 ;
;
Соответственно, 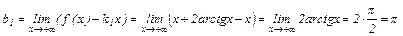 .
.
Таким образом, 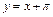 – правая наклонная асимптота.
– правая наклонная асимптота.
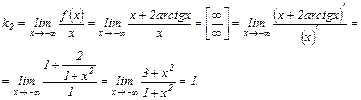
Соответственно, 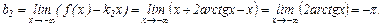
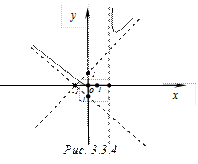
Таким образом, 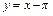 – левая наклонная асимптота (рис.4.3.3).
– левая наклонная асимптота (рис.4.3.3).
|
2) Функция определена в интервалах 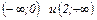 .
.
Так как
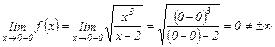 ,
,
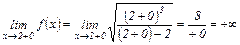 ,
,
то только прямая 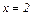 является вертикальной асимптотой.
является вертикальной асимптотой.
Исследуем поведение функции при 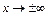 , т. е. найдём наклонные (горизонтальные) асимптоты
, т. е. найдём наклонные (горизонтальные) асимптоты 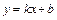 .
.
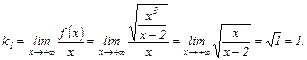
Соответственно, 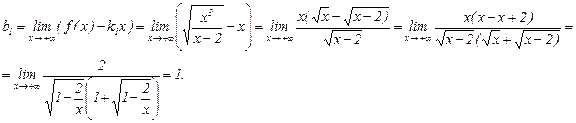

Таким образом, существует правая наклонная асимптота 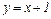 .
.
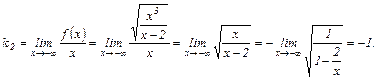
Соответственно, 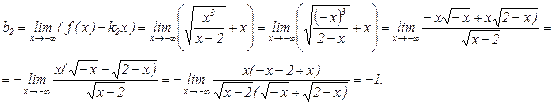


Таким образом, правая наклонная асимптота 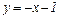 (рис. 4.3.4).
(рис. 4.3.4).
|
| <== предыдущая лекция | | | следующая лекция ==> |
| Топперы | | | Урок № 2 |
Дата добавления: 2014-12-01; просмотров: 1211;
