Задача 4.1.
ПРИМЕНЕНИЕ ПРЕОБРАЗОВАНИЙ ЛАПЛАСА ПРИ РАСЧЕТЕ ПЕРЕХОДНЫХ РЕЖИМОВ ЛИНЕЙНЫХ ЦЕПЕЙ С ИСТОЧНИКАМИ ПОСТОЯННЫХ ЭДС
1. Исходные данные
Исходные данные те же, что в задаче 4.
2. Задание
2.1. Начертить операторную схему для свободных составляющих.
2.2. Определить закон изменения свободной составляющей тока в ветви |c - d|, применив преобразования Лапласа.
3. Методические указания
3.1. В операторной схеме (п.2.1) имеются лишь операторные ЭДС, учитывающие свободные составляющие независимых начальных условий.
3.2. Независимые начальные условия определены в задаче 1.
3.3. Для получения оригинала рекомендуется использовать теорему о вычетах (формулу разложения).
3.4. Проверкой правильности решения задач 10 и 11 может служить соответствие результатов их решения.
ПРИМЕРЫ
Пример 1
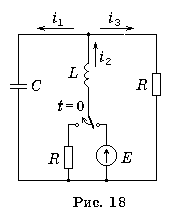
В схеме рис.18 E = 12 B, R = 120 Ом, L = 10 мГн, С = 5 мкФ. В момент t = 0 мгновенно осуществляется коммутация. Определить закон изменения свободной составляющей тока i3(t) , применив преобразования Лапласа.
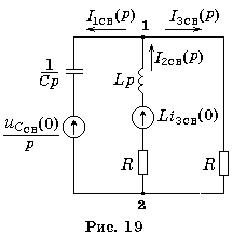
Операторная схема для свободных составляющих представлена на рис.19 при выбранных направлениях токов.
Независимые начальные условия определяются по схеме рис.18:
i2(0+) = i2(0-) = 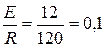 А,
А,
uC(0+) = uC (0-) = Е = 12 В.
| 
|
В данном случае принужденные составляющие отсутствуют, следовательно, i2СВ(0) = i2(0) - i2ПР(0) = 0,1 - 0 = 0,1 А, uCСВ(0) = 12 В, а, например, I3СВ(р) = I3(р).
Для определения тока I3СВ(р) целесообразно применить метод эквивалентного источника или метод узловых потенциалов. Согласно методу двух узлов
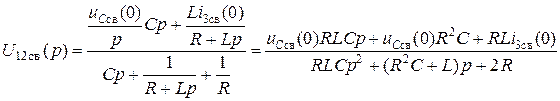 ,
,
Операторный ток
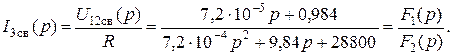
Согласно формуле разложения оригинал тока
i3св (t) = 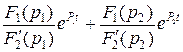 ,
,
где корни уравнения F2(р) = 0 p1 = -4250 с-1 , p2 = -9417 с-1 , а
F1(р1) = 0,678, F1(р2) = 0,306, F¢2(р) = 1,44·10-3р+9,84 , F¢2(р1) = 3,72,
F¢2( р2 ) = -3,78.
Окончательно
i3св (t) = 0,182 е-4250 t - 0,0822 е-9417 t А.
Дата добавления: 2014-12-06; просмотров: 760;
