Пример 2. Классический метод расчета переходного режима
Классический метод расчета переходного режима
Исходные данные
Составляем схему электрической цепи и рассчитываем её элементы в соответствии с условием задачи и сформированным кодом (рис.1):
| a | b | c | d | e | f |
E = 10·e = 10·1 = 10 B
R = 10·b·f = 10·3·2 = 60 Ом
R1 = 90·b·f = 90·3·2 = 540 Ом
L = 1.25·d = 1.25·4 = 5 мГн = 5E-3 Гн
С = 1,0·d = 1.0·4 = 4 мкФ = 4E-6 Ф
Задание
1.Определить закон изменения тока в ветви |c - d| = |3 - 4| = 1, применив классический метод расчета.
2.Построить график найденного тока.
В схеме цепи рис.1 в момент t = 0 мгновенно осуществляется коммутация. Определить закон изменения тока i1 (t).
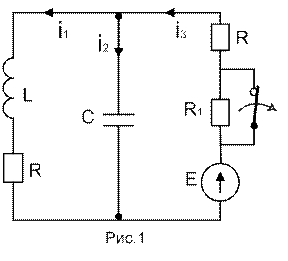
Переходной процесс в цепи при выбранных направлениях токов описывается тремя уравнениями:
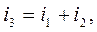 (1)
(1)
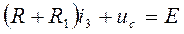 , (2)
, (2)
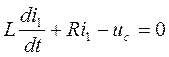 , (3)
, (3)
где 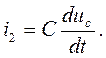 (4)
(4)
Искомый ток
i1 = i1ПР + i1СВ (5)
Принужденное значение тока
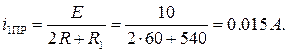
Выражение для свободной составляющей определяется корнями характеристического уравнения:
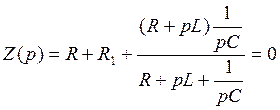
или 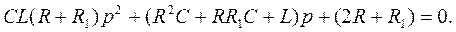
Решая это уравнение, получаем:
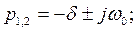
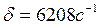 ,
,  ,
, 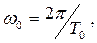
где δ – коэффициент затухания;
ω0 - угловая частота собственных колебаний;
Т0 – период собственных колебаний.
В этом случае 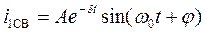 , а полный ток:
, а полный ток:
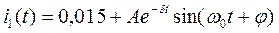 .
.
Определяем постоянные интегрирования с учетом начальных условий. В соответствии с первым законом коммутации 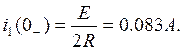
Тогда 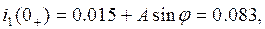
откуда  А = 0,068/sin φ.
А = 0,068/sin φ.
Второе уравнение, связывающее постоянные интегрирования А и φ, получаем из выражения первой производной:
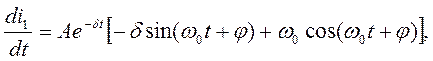
имеющей для t = 0 следующий вид:
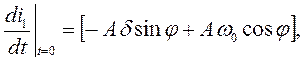
Начальное значение производной определяем из уравнения (3):
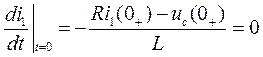 ,
,
где i1(0+) = 0.083; uc(0+) = R i1(0-) =5 В (по законам коммутации).
Тогда получаем: tgφ = ω0/δ; φ = arctg (ω0/δ) = 33.160; A = 0.124.
Таким образом, окончательно получаем выражение для тока в первой ветви:
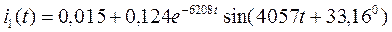 А.
А.
Определяем постоянную времени τ период собственных колебаний Т0:
τ = 1/δ = 1/6208 = 0,16 мС; Т0 = 2π/ω0 = 2π/4057 = 1,55 мС.
Подставляя полученные значения, получаем следующее выражение для тока в первой ветви:
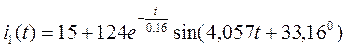 мА.
мА.
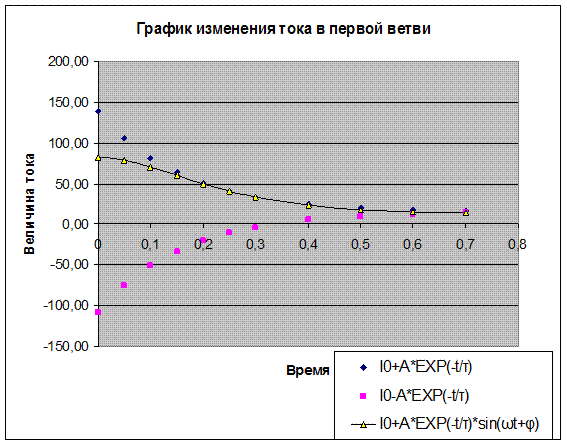
Построим осциллограмму найденного тока для интервала времени
о < t < 4τ = 0.7 мC с помощью EXCEL:
| Таблица расчета изменения тока в первой ветви | |||||||||||
| Время t,мС | 0,05 | 0,1 | 0,15 | 0,2 | 0,25 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | |
| I0+A*EXP(-t/τ) | 139,00 | 105,72 | 81,37 | 63,56 | 50,53 | 40,99 | 34,02 | 25,18 | 20,45 | 17,92 | 16,56 |
| I0-A*EXP(-t/τ) | -109,00 | -75,72 | -51,37 | -33,56 | -20,53 | -10,99 | -4,02 | 4,82 | 9,55 | 12,08 | 13,44 |
| I0+A*EXP(-t/τ)*sin(ωt+φ) | 82,83 | 78,90 | 70,29 | 60,03 | 49,95 | 40,99 | 33,54 | 23,22 | 17,77 | 15,37 | 14,57 |
Определение тока во второй ветви
Закон изменения тока во второй ветви определяется уравнением:
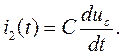
Находим закон изменения напряжения на конденсаторе:
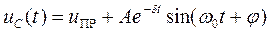 ,
,
где 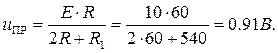
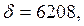
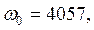
Определяем постоянные интегрирования с учетом начальных условий.
В соответствии со вторым законом коммутации 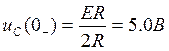
Тогда 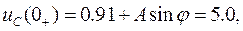
откуда  А = 4,09/sin φ.
А = 4,09/sin φ.
Второе уравнение, связывающее постоянные интегрирования А и φ, получаем из выражения первой производной:
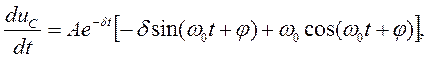
имеющей для t = 0 следующий вид:
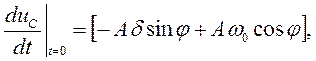
Начальное значение производной определяем из уравнения (4):
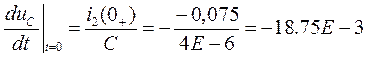 ,
,
где из уравнения (1): 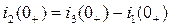 ,
,
из уравнения (2): 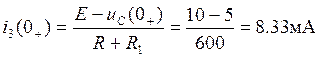 ,
,
в соответствии с первым законом коммутации 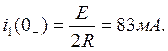
Тогда получаем: φ = 68,190; A = 4.41.
Таким образом, окончательно получаем выражение для напряжения:
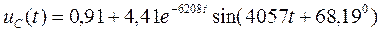 А.
А.
Определяем постоянную времени τ период собственных колебаний Т0:
τ = 1/δ = 1/6208 = 0,16 мС; Т0 = 2π/ω0 = 2π/4057 = 1,55 мС.
Подставляя полученные значения, получаем следующее выражение для напряжения на конденсаторе:
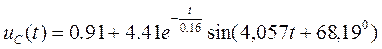 В.
В.
Закон изменения тока во второй ветви определяется уравнением:
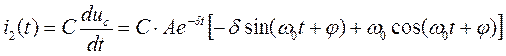 .
.
Подставляя численные значения параметров, получаем:
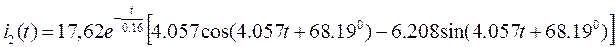 мА.
мА.
Преобразуя полученное выражение, окончательно получаем:
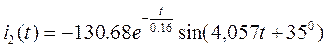 мА.
мА.
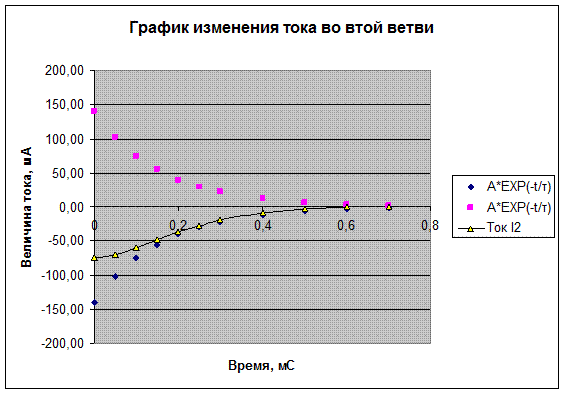
Строим осциллограмму найденного тока для интервала времени
о < t < 4τ = 0.7 мC с помощью EXCEL:
| Время t,мС | 0,05 | 0,1 | 0,15 | 0,2 | 0,25 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | |
| A*EXP(-t/τ) | -140,00 | -102,43 | -74,94 | -54,82 | -40,11 | -29,35 | -21,47 | -11,49 | -6,15 | -3,29 | -1,76 |
| A*EXP(-t/τ) | 140,00 | 102,43 | 74,94 | 54,82 | 40,11 | 29,35 | 21,47 | 11,49 | 6,15 | 3,29 | 1,76 |
| Ток I2 | -75,08 | -69,59 | -59,56 | -48,11 | -37,07 | -27,38 | -19,40 | -8,46 | -2,76 | -0,30 | 0,50 |
Определение тока в третьей ветви
Закон изменения тока во второй ветви определяется с учетом уравнения (2).
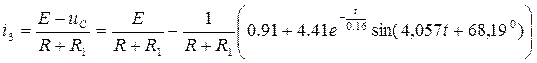 .
.
Окончательно получаем выражение для тока в третьей ветви:
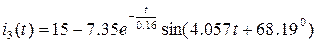 .
.
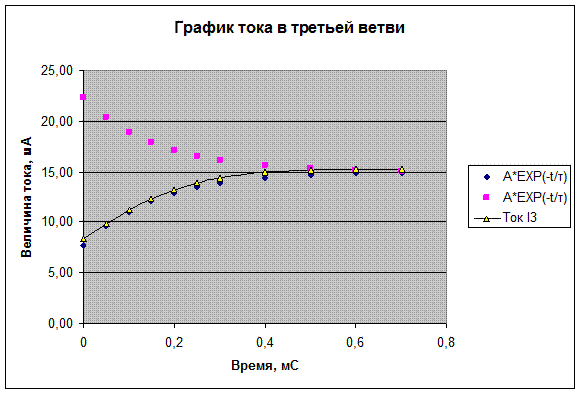
Строим осциллограмму найденного тока для интервала времени
о < t < 4τ = 0.7 мC с помощью EXCEL:
| Время t,мС | 0,05 | 0,1 | 0,15 | 0,2 | 0,25 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | |
| A*EXP(-t/τ) | 7,65 | 9,62 | 11,07 | 12,12 | 12,89 | 13,46 | 13,87 | 14,40 | 14,68 | 14,83 | 14,91 |
| A*EXP(-t/τ) | 22,35 | 20,38 | 18,93 | 17,88 | 17,11 | 16,54 | 16,13 | 15,60 | 15,32 | 15,17 | 15,09 |
| Ток I3 | 8,33 | 9,86 | 11,22 | 12,35 | 13,24 | 13,91 | 14,39 | 14,96 | 15,17 | 15,23 | 15,22 |
Осуществляем проверку 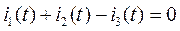 в рассчитанных точках:
в рассчитанных точках:
| Проверка ΣI | -0,58 | -0,55 | -0,49 | -0,42 | -0,36 | -0,30 | -0,26 | -0,20 | -0,17 | -0,15 | -0,15 |
Дата добавления: 2014-12-06; просмотров: 1979;
