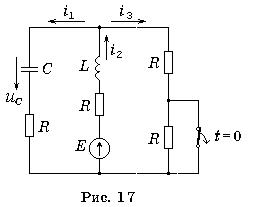
Пример 1. В схеме цепи рис.17 в момент t = 0 мгновенно осуществляется коммутация
В схеме цепи рис.17 в момент t = 0 мгновенно осуществляется коммутация. Е = 18 В, R = 60 Ом, L = 10 мГн, С = 5 мкФ. Определить закон изменения тока i3 (t).
Переходной процесс в цепи при выбранных направлениях токов описывается тремя уравнениями:
| i2 = i1 + i3 , (1)
Ri2 + L 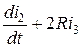 = Е, (2)
2Ri3 = uс + Ri1 , (3)
где
i1 = С = Е, (2)
2Ri3 = uс + Ri1 , (3)
где
i1 = С 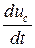 . (4)
Искомый ток
i3 = i3ПР +i3СВ . (5) . (4)
Искомый ток
i3 = i3ПР +i3СВ . (5)
|
Принужденное значение тока
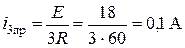 .
.
Выражение для свободной составляющей определяется корнями характеристического уравнения:
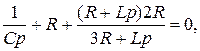
откуда
p1 = - 2260 с-1, p2 = - 8850 с-1 .
При двух различных вещественных корнях i3СВ = А1еP1t + А2еP2t .
Постоянные интегрирования находятся при учете начальных условий:
i3СВ(0) = А1 + А2, i¢3СВ(0) = р1А1 + р2А2 . (6)
Оба начальных условия зависимые и находятся из уравнений Кирхгофа (1) - (3) с учетом независимых начальных условий.
Независимые начальные условия определяются установившимся режимом до коммутации:
i2(0+) = i2(0-) = 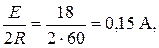
uc(0+) = uc(0-) = Ri3(0-) = Ri2(0-) = 60 · 0,15 = 9 В.
При данных i2(0) и uc(0) из уравнений (1), (3)
i2(0) = i1(0) + i3(0) , 2Ri3(0) = uc(0) + Ri1(0) .
Отсюда значения токов i3(0) = 0,1 А, i1(0) = 0,05 А. Из уравнения (2) i2¢ (0) = - 300 А/c. Дифференцирование уравнений (1), (3) с учетом уравнения (4) позволяет найти второе зависимое начальное условие:
 i¢2(0) = i¢1(0) + i¢3(0) , 2Ri¢3(0) =
i¢2(0) = i¢1(0) + i¢3(0) , 2Ri¢3(0) = 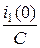 + Ri¢1(0) ,
+ Ri¢1(0) ,
т.е. i¢3(0) = - 44,4 А/с.
Подстановка полученных результатов в выражение (6) дает А1 = - 6,74·10-3 А, А2 = 6,74 · 10-3 А, а в выражение (5) - окончательный результат
i3(t) = 0,1 - 6,74 · 10-3 е-2260 t + 6,74 · 10-3 е-8850 t А.
Дата добавления: 2014-12-06; просмотров: 998;
