Определенный интеграл. Определение 3. Если функция непрерывна на промежутке [a;b] числовой оси, содержащей точки x=a и x=b
Определение 3. Если функция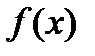 
непрерывна на промежутке [a;b] числовой оси, содержащей точки x=a и x=b, то разность значений 
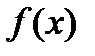для функции называется определенным интегралом от функции 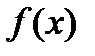от a до b. 
- формула Ньютона – Лейбница
а- нижний предел интегрирования, в- верхний передел интегрирования
Пример: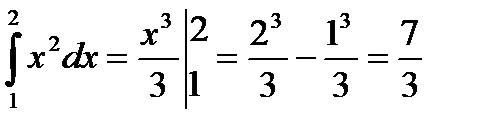 
Дата добавления: 2014-12-05; просмотров: 834;