Одной переменной.
Основные теоретические сведения.
1. Производной функции 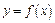 по аргументу x называется предел отношения приращения функции к приращению независимого аргумента при условии, что приращение аргумента стремится к нулю. Производная функции
по аргументу x называется предел отношения приращения функции к приращению независимого аргумента при условии, что приращение аргумента стремится к нулю. Производная функции 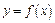 обозначается через
обозначается через 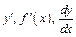 .
.
По определению: 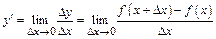 .
.
Операция отыскания производной заданной функции называется дифференцированием этой функции. По определению можно получить следующую таблицу формул дифференцирования элементарных функций:
1. 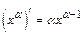 , где
, где 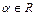 ; 8)
; 8) 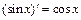 ;
;
2. 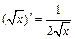 ; 9)
; 9)  ;
;
3. 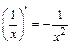 ; 10)
; 10) 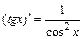 ;
;
4.  ; 11)
; 11) 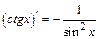 ;
;
5. 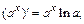 12)
12) 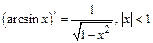 ;
;
6. 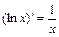 ; 13)
; 13) 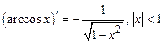 ;
;
7. 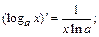 14)
14)  ;
;
15) 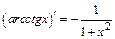 .
.
Кроме того существуют следующие правила дифференцирования. Пусть С 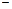 постоянная, u=u(x), v=v(x)
постоянная, u=u(x), v=v(x) 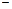 функции, имеющие производные. Тогда:
функции, имеющие производные. Тогда:
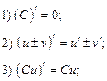
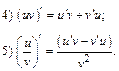
Рассмотренных формул и правил определения производных недостаточно для нахождения производных функций более сложного вида, например, таких как  и т.д.
и т.д.
Пусть y–есть функция от u:  , где u–в свою очередь функция от аргумента x:
, где u–в свою очередь функция от аргумента x: 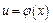 ; в таком случае говорят, что y есть функция от функции, т.е.
; в таком случае говорят, что y есть функция от функции, т.е.  .
.
Если для соответствующих друг другу значений x и u существуют производные 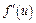 и
и 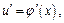 то существует и производная от y по x, причем имеет место равенство
то существует и производная от y по x, причем имеет место равенство
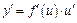 . (1)
. (1)
2.Дифференцирование функций, заданных параметрически.
Пусть функция 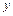 аргумента x задана при помощи параметрических соотношений
аргумента x задана при помощи параметрических соотношений 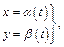 причем
причем 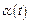 и
и  дифференцируемые функции от t и
дифференцируемые функции от t и 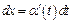 ,
,  . Тогда
. Тогда
 . (2)
. (2)
3.Правило Лопиталя. Предел отношения двух бесконечно малых или бесконечно больших функций (неопределенность 0/0 или  ) равен пределу отношения их производных:
) равен пределу отношения их производных:
 (3)
(3)
если предел справа существует.
Дата добавления: 2014-12-03; просмотров: 1342;
