Относительное движение материальной точки

Если материальная точка массой m движется в подвижной системе координат, то такое движение называется относительным (ч. 2, п. 2.5.1). В этом случае основное уравнение динамики, в отличие от абсолютного движения относительно неподвижной системы координат (инерциальной системы отсчета, п. 3.1.2), имеет вид:

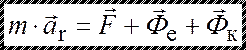
и называется основным уравнением динамики относительного движения материальной точки. Здесь 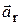- относительное ускорение точки, 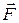- геометрическая сумма всех действующих на точку активных сил и реакций связей, 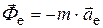- переносная сила инерции ( 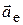- переносное ускорение), 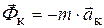- кориолисова сила инерции ( 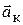- ускорение Кориолиса).

Таким образом, относительное движение материальной точки исследуется так же, как движение абсолютное ( 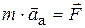), только к активным силам и реакциям связей добавляются переносная 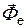и кориолисова 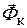силы инерции материальной точки.

Из основного уравнения динамики относительного движения так же, как для движения абсолютного (п. 3.2.1), в проекциях на оси координат получаются дифференциальные уравнения относительного движения материальной точки. В общем случае они включают в себя проекции переносной 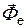и кориолисовой 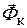сил инерции на соответствующие оси координат. При исследовании относительного движения так же, как для движения абсолютного (п. 3.2.2), решаются прямая (определение сил) и обратная (определение движений) задачи динамики относительного движения.