Принцип относительности классической механики

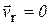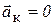Если точка не движется в подвижной системе координат (нет относительного движения), то относительная скорость точки , относительное ускорение , ускорение Кориолиса (ч. 2, п. 2.5.3), кориолисова сила инерции 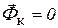, и основное уравнение динамики относительного движения (п. 3.8.3) имеет вид: 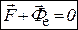. Это векторное равенство представляет собой уравнение относительного равновесия материальной точки. Его смысл состоит в том, что относительное равновесие материальной точки исследуется так же, как равновесие абсолютное ( 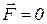), только к активным силам и реакциям связей добавляется переносная сила инерции 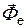материальной точки.

Если переносное движение (движение подвижной системы координат по отношению к неподвижной) является поступательным, то ускорение Кориолиса 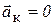(ч. 2, п. 2.5.3), кориолисова сила инерции 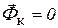, и основное уравнение динамики относительного движения (п. 3.8.3) имеет вид: .

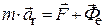Если переносное движение является поступательным, равномерным и прямолинейным, то кориолисова сила инерции 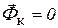, переносная сила инерции 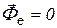, в этом случае основное уравнение динамики относительного движения 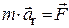и абсолютного движения 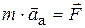одинаковы (инвариантны). Этот результат представляет собой принцип относительности классической механики(принцип Галилея-Ньютона): никакими механическим опытами нельзя обнаружить, находится ли данная система отсчета в покое или же совершает поступательное, равномерное и прямолинейное движение.

Принцип относительности классической механики можно сформулировать иначе: любая система отсчета, движущаяся по отношению к инерциальной поступательно, равномерно и прямолинейно, тоже является инерциальной.