Динамические реакции
Одно из многих практических приложений принципа Даламбера – определение динамических реакций движущихся тел, механических систем, систем тел.
Например, определение реакций 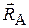 подпятника А и
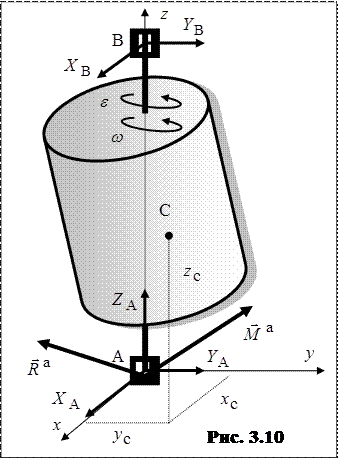
подпятника А и 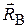 подшипника В для вращающегося относительно неподвижной оси тела (рис. 3.10). Пусть АВ=Н, M – масса,
подшипника В для вращающегося относительно неподвижной оси тела (рис. 3.10). Пусть АВ=Н, M – масса, 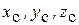 - координаты центра масс С тела,
- координаты центра масс С тела, 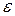 - угловое ускорение,
- угловое ускорение, 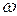 - угловая скорость тела в данный момент времени,
- угловая скорость тела в данный момент времени, 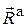 - главный вектор,
- главный вектор, 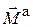 - главный момент активных (задаваемых) сил, действующих на тело. С помощью принципа Даламбера можно составить три уравнения динамического равновесия в проекциях на координатные оси:
- главный момент активных (задаваемых) сил, действующих на тело. С помощью принципа Даламбера можно составить три уравнения динамического равновесия в проекциях на координатные оси:
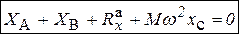 ,
, 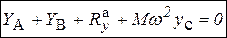 ,
, 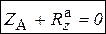
и три уравнения равновесия моментов относительно координатных осей:
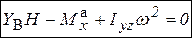 ,
, 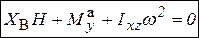 ,
, 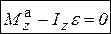 .
.
Последнее уравнение не содержит реакций, из него можно найти угловое ускорение 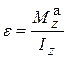 , которое зависит от активных (задаваемых) сил и осевого момента инерции
, которое зависит от активных (задаваемых) сил и осевого момента инерции 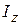 тела. Другие уравнения дают возможность найти все составляющие
тела. Другие уравнения дают возможность найти все составляющие 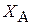 ,
, 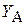 ,
, 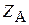 ,
, 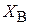 ,
, 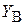 реакций подпятника А и подшипника В.
реакций подпятника А и подшипника В.
1. Если угловая скорость тела 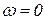 , получатся обычные уравнения статического равновесия для определения статических реакций.
, получатся обычные уравнения статического равновесия для определения статических реакций.
2. Реакции опор вращающегося тела не зависят от углового ускорения 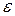 , но зависят от величины угловой скорости
, но зависят от величины угловой скорости 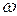 тела.
тела.
3. Динамические реакции зависят от центробежных моментов инерции тела 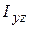 и
и 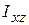 .
.
4.  Если центр масс находится на оси вращения (
Если центр масс находится на оси вращения ( 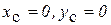 ), центробежные моменты инерции
), центробежные моменты инерции 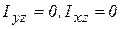 , то вращение тела не влияет на реакции.
, то вращение тела не влияет на реакции.
5. Динамические реакции зависят от центробежных моментов инерции тела 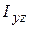 и
и 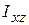 .
.
6. Если центр масс находится на оси вращения ( 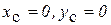 ), центробежные моменты инерции
), центробежные моменты инерции 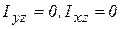 , то вращение тела не влияет на реакции.
, то вращение тела не влияет на реакции.
Проходящая через центр масс тела ось z, для которой центробежные моменты инерции 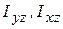 , содержащие в своих индексах наименование данной оси, равны нулю, называется главной центральной осью тела. Вращающееся тело, реакции опор которого не зависят от величины угловой скорости, называется динамически уравновешенным. Условие динамической уравновешенности вращающегося тела: ось вращения тела должна быть одной из главных центральных
, содержащие в своих индексах наименование данной оси, равны нулю, называется главной центральной осью тела. Вращающееся тело, реакции опор которого не зависят от величины угловой скорости, называется динамически уравновешенным. Условие динамической уравновешенности вращающегося тела: ось вращения тела должна быть одной из главных центральных 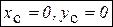 ,
, 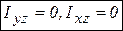 . Уравновешенности вращающихся тел можно добиться динамической балансировкой. Основной принцип динамической балансировки: добавлением (или удалением) двух точечных масс, лежащих в произвольно выбранных плоскостях, перпендикулярных оси вращения тела, ее всегда можно сделать главной центральной осью тела.
. Уравновешенности вращающихся тел можно добиться динамической балансировкой. Основной принцип динамической балансировки: добавлением (или удалением) двух точечных масс, лежащих в произвольно выбранных плоскостях, перпендикулярных оси вращения тела, ее всегда можно сделать главной центральной осью тела.
Дата добавления: 2014-12-01; просмотров: 5873;
