Классификация связей. Идеальные связи

Наложенные на механическую систему связи могут быть заданы аналитически своими уравнениями.

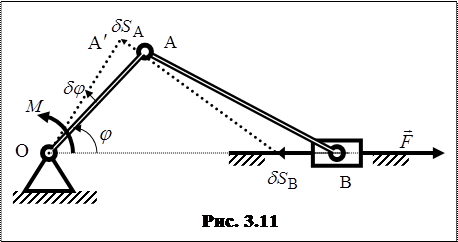
Например, для кривошипно-шатунного механизма (рис. 3.11): 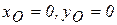- уравнения неподвижного подшипника О, относительно которого вращается кривошип ОА; 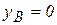- уравнение направляющей ползуна В; 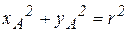- уравнение недеформируемости кривошипа ОА = r; 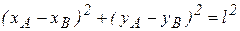- уравнение недеформируемости шатуна АВ = l.

В общем случае уравнение любой связи можно представить в виде функции координат 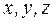, скоростей 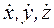точек системы и времени t: .

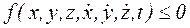1. Если уравнение связи содержит равенство (=), связь удерживающая, если содержит неравенство ( 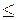) – неудерживающая.

2. Если уравнение не содержит время t, связь стационарная, если содержит – нестационарная.

3. Если уравнение не содержит скорости 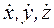, связь геометрическая, если содержит – кинематическая.

Все внешние и внутренние связи кривошипно-шатунного механизма (рис. 3.11), в соответствии с видом их уравнений – удерживающие, стационарные, геометрические. В дальнейшем рассматриваются системы только с такими связями.

Особый вид классификации связей – деление их на идеальные и неидеальные. Идеальными называются связи, сумма элементарных работ реакций которых на любом возможном перемещении системы равна нулю. Аналитическое условие идеальной связи: 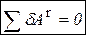. В противном случае связь является неидеальной.

Основные виды идеальных связей - гладкая поверхность, неподвижный шарнир или подшипник без трения, шероховатая поверхность при качении тела без скольжения, внутренние связи абсолютно твердого тела.