Принцип Даламбера-Лагранжа

Принцип Даламбера (п. 3.8) позволяет любую задачу динамики решать как задачу о равновесии. Если для решения задачи о динамическом равновесии применить принцип возможных перемещений (п. 3.9), получится новый метод решения задач динамики, который называется принципом Даламбера-Лагранжа.

Принцип Даламбера-Лагранжа. При движении механической системы с наложенными на нее идеальными связями сумма элементарных работ всех активных сил и сил инерции на любом возможном перемещении равна нулю:

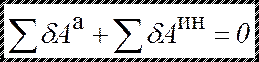
Это уравнение называется общим уравнением динамики или уравнением работ.

С учетом разных способов определения элементарной работы силы (табл. 3.3) общее уравнение динамики можно записать и использовать в разных формах: векторная 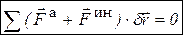, координатная 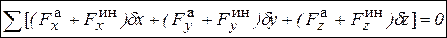, естественная .

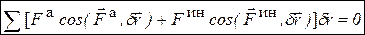В случае, когда среди связей, наложенных на механическую систему, есть неидеальные, при использовании общего уравнения динамики надо включить в него работу реакций неидеальных связей. Приняв общее уравнение динамики за исходное, можно вывести из него все основные теоремы динамики (п. 3.4, 3.5, 3.6).

Общее уравнение динамики позволяет также составить дифференциальные уравнения движения любой механической системы. Они составляются по каждому из независимых возможных перемещений (п. 3.9.1), поэтому количество уравнений движения равно числу степеней свободы механической системы. Но более рациональным подходом в этом случае является использование уравнений Лагранжа второго рода (п. 3.11) - дифференциальных уравнений движения механической системы в обобщенных силах.