Динамическое исследование движения системы грузов
Пусть дана система трех грузов массами 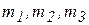 , которые связаны между собой невесомыми тросами, перекинутыми через невесомые блоки (рис. 3.12). Чтобы найти ускорения грузов, можно использовать общее уравнение динамики (п. 3.10.1).
, которые связаны между собой невесомыми тросами, перекинутыми через невесомые блоки (рис. 3.12). Чтобы найти ускорения грузов, можно использовать общее уравнение динамики (п. 3.10.1).
Механическая система имеет две степени свободы. За обобщенные координаты выбраны: линейная координата  (определяет абсолютное положение груза 1) и линейная координата
(определяет абсолютное положение груза 1) и линейная координата 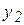 (определяет относительное положение груза 2). Так как связи идеальные, в уравнении работ учитываются только активные силы – силы тяжести
(определяет относительное положение груза 2). Так как связи идеальные, в уравнении работ учитываются только активные силы – силы тяжести 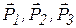 , и силы инерции грузов –
, и силы инерции грузов – 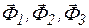 . При этом силы инерции выражаются через абсолютные ускорения грузов:
. При этом силы инерции выражаются через абсолютные ускорения грузов: 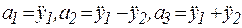 .
.
По каждой из двух обобщенных координат записываются уравнения работ на возможных бесконечно малых перемещениях:
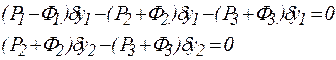
В результате получается система двух уравнений с двумя неизвестными обобщенными ускорениями 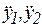 :
:
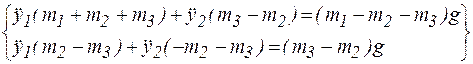 .
.
Решив эту систему, можно найти обобщенные ускорения и абсолютные ускорения всех трех грузов:
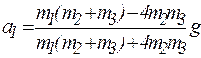

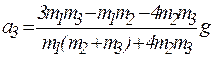 .
.
Принцип возможных перемещений (п. 3.9.3) или общее уравнение статики в обобщенных силах (п. 3.10.3) для системы с двумя степенями свободы приводит к двум уравнениям равновесия: 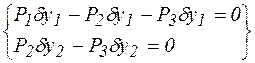 , откуда получаются условия равновесия системы:
, откуда получаются условия равновесия системы: 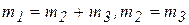 .
.
Дата добавления: 2014-12-01; просмотров: 1266;
