Эллиптический маятник
Механическая система состоит из двух точечных масс 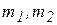 , связанных невесомым стержнем длиной l (рис. 3.13). Для исследования движения системы с двумя степенями свободы выбраны две обобщенные координаты – линейная координата x, определяющая положение груза
, связанных невесомым стержнем длиной l (рис. 3.13). Для исследования движения системы с двумя степенями свободы выбраны две обобщенные координаты – линейная координата x, определяющая положение груза 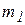 , и угловая координата
, и угловая координата  , определяющая угол поворота стержня.
, определяющая угол поворота стержня.
Кинетическая энергия системы:
 .
.
Обобщенные силы: 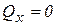 ,
, 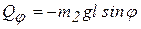 .
.
Уравнения Лагранжа второго рода (п. 3.11.1) дают два дифференциальных уравнения по каждой из двух обобщенных координат:
 .
.
 Эти уравнения полностью описывают движение механической системы. Однако, их решение вызывает определенные математические сложности. Пусть координата
Эти уравнения полностью описывают движение механической системы. Однако, их решение вызывает определенные математические сложности. Пусть координата 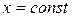 , угол
, угол  является малым, тогда из второго уравнения получается дифференциальное уравнение малых колебаний математического маятника
является малым, тогда из второго уравнения получается дифференциальное уравнение малых колебаний математического маятника 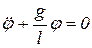 . Такое уравнение можно решить как уравнение свободных колебаний материальной точки (п. 3.2.6).
. Такое уравнение можно решить как уравнение свободных колебаний материальной точки (п. 3.2.6).
ОСНОВНАЯ УЧЕБНАЯ ЛИТЕРАТУРА
1. Бутенин Н.В., Лунц Я.Л., Меркин Д.Р. Курс теоретической механики: В 2-х томах. Т. 1. Статика и кинематика. – 3-е изд., стереотип. – М.: Наука, 1979. – 272 с. Т. 2. Динамика. – 2-е изд., перераб. и доп. – М.: Наука, 1979. – 544 с. (и другие издания).
2. Гернет М.М. Курс теоретической механики. – 4-е изд., перераб. и сокр. – М.: Высшая школа, 1981. – 304 с. (и другие издания).
3. Лойцянский Л.Г., Лурье А.И. Курс теоретической механики: В 2-х томах. Т. 1. Статика и кинематика. – 8-е изд., перераб. и доп. – М.: Наука, 1982. – 352 с. Т. 2. Динамика. – 6-е изд., перераб. и доп. – М.: Наука, 1983. – 640 с. (и другие издания).
4. Никитин Е.М. Краткий курс теоретической механики. - М.: Наука, 1971. – 400 с. (и другие издания).
5. Тарг С.М. Краткий курс теоретической механики. – 11-е изд., испр. – М.: Высшая школа, 1995. – 416 с. (и другие издания).
6. Яблонский А.А., Никифорова В.М. Курс теоретической механики: В 2-х частях. Ч. 1. Статика и кинематика. – 6-е изд., испр. – М.: Высшая школа, 1984. – 368 с. Ч. 2. Динамика. – 6-е изд., испр. – М.: Высшая школа, 1984. – 412 с. (и другие издания).
Дата добавления: 2014-12-01; просмотров: 2113;
