Возможные перемещения механической системы

Возможными (или виртуальными) перемещениями называются воображаемые бесконечно малые перемещения механической системы, допускаемые в данный момент времени наложенными на систему внешними и внутренними связями.

В отличие от действительных бесконечно малых перемещений, обозначаемых символом дифференциала d (например, 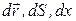), возможные перемещения обозначаются символом вариации 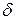( 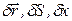), хотя математически вариации 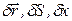и дифференциалы 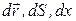перемещений определяются одинаково. Действительное перемещение 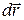какой-либо точки механической системы всегда одно, возможных перемещений 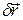у нее может быть больше, чем одно, в том числе - бесчисленное множество. В случае стационарных связей (то есть связей, свойства которых не зависят от времени, п. 3.9.2) действительное перемещение 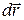точки есть одно из ее возможных перемещений .

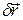Например, для кривошипно-шатунного механизма (рис. 3.11) возможными перемещениями точки В (ползуна) являются два бесконечно малых перемещения 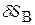вдоль горизонтальной направляющей – в одну или другую сторону. Действительное бесконечно малое перемещение 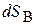- одно из них. Поскольку возможные перемещения являются бесконечно малыми, то криволинейные перемещения точек (например, точки А кривошипа ОА) по дуге окружности можно заменить прямолинейными перемещениями по касательной к траектории точки: 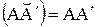( 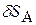на рис. 3.11).

Возможные перемещения системы ограничены наложенными на нее связями, поэтому для определения положения точек системы нет необходимости знать координаты всех точек. Например, положение всех звеньев и точек кривошипно-шатунного механизма (рис. 3.11) вполне определяется заданием только одного угла 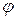поворота кривошипа. Координаты всех точек этого механизма могут быть выражены в функции от одной независимой переменной – угла 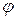. Механическую систему, положение которой однозначно определяется заданием одним геометрическим параметром (линейной или угловой координатой), называют системой с одной степенью свободы.

Для определения положения точки в пространстве надо задать не одну, а три координаты – например, 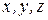в прямоугольной декартовой системе координат. Независиые геометрические параметры (как правило, линейные и угловые координаты), заданием которых однозначно определяется положение механической системы, называются обобщенными координатами механической системы. Число обобщенных координат называется числом степеней свободы механической системы. Число независимых между собой возможных перемещений равно числу степеней свободы механической системы.