Принцип Даламбера для механической системы

Принцип Даламбера для механической системы. В каждый данный момент времени при движении механической системы геометрическая сумма всех активных сил, реакций связей и главного вектора сил инерции равна нулю:

,

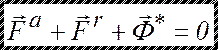а также геометрическая сумма моментов всех активных сил, моментов реакций связей и главного момента сил инерции относительно любого центра О равна нулю:

.

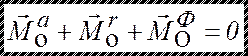При решении задач динамики механической системы принципом Даламбера в общем случае из первого векторного уравнения получаются три уравнения равновесия в проекциях на три координатные оси, из второго векторного равенства – еще три уравнения равновесия в форме уравнений моментов относительно трех координатных осей, всего – шесть уравнений динамического равновесия (ч. 1, п. 1.5.5).

Фактически это означает, что любую задачу динамики механической системы можно решить как задачу о равновесии. Для этого к активным силам и реакциям связей в расчетную схему сил необходимо добавить главный вектор и главный момент сил инерции механической системы.