Качение тела по наклонной плоскости

По шероховатой наклонной плоскости катится без скольжения однородный диск, коэффициент трения качения 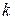. Масса диска M, радиус R.. К центру С диска приложена постоянная по величине сила 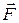, направленная вверх вдоль наклонной плоскости (рис. 3.8, а). Найти ускорение центра С диска.

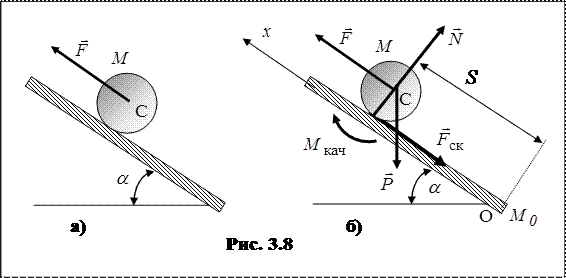
При качении по плоскости диск совершает плоскопараллельное движение. Так как поступательное движение вместе с центром С является прямолинейным, из трех дифференциальных уравнений плоского движения (п. 3.7.3) остаются два – в поступательном и вращательном движениях. При составлении уравнений учитываются все внешние силы, действующие на тело (рис. 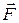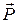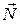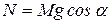3.8, б): заданная сила , сила тяжести тела (по модулю ), нормальная реакция плоскости ( ), неизвестная по величине сила трения скольжения 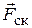и момент трения качения .

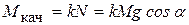Дифференциальные уравнения движения диска имеют вид: 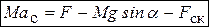- в поступательном движении в проекции на направление движения (ось x), 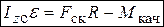- во вращательном движении. Угловое ускорение 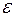и ускорение 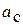центра при качении диска без скольжения связаны зависимостью 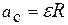, осевой момент инерции однородного диска (п. 3.3.2, табл. 3.2) .

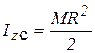Решая совместно эти два уравнения, можно получить ускорение центра диска 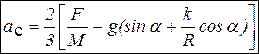и силу трения скольжения 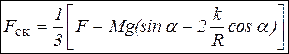. Из условия, что сила трения скольжения равна 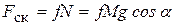, можно найти минимальный коэффициент трения скольжения 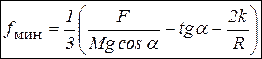, обеспечивающий качение диска по плоскости без скольжения.

Ускорение 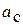можно получить, используя теорему об изменении кинетической энергии. Изменение кинетической энергии на перемещении 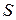центра С диска из начального (состояние покоя) в конечное (произвольное, текущее) положение равно сумме работ сил, действующих на тело, на том же перемещении: .

Дифференцируя по времени это уравнение с учетом связи между скоростью 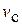и угловой скоростью 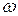диска 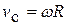, а также между перемещением 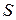центра С и углом 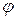поворота диска 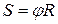, можно найти то же ускорение 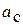центра С диска.