Скольжение тела по наклонной плоскости
По шероховатой наклонной плоскости пущено вверх со скоростью 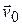 тело массой М, коэффициент трения скольжения
тело массой М, коэффициент трения скольжения 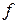 . Во все время движения на тело действует постоянная по величине сила
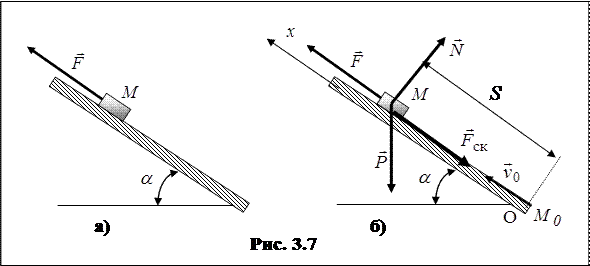
. Во все время движения на тело действует постоянная по величине сила 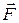 , направленная вверх по наклонной плоскости (рис. 3.7, а). Найти ускорение и закон движения тела по плоскости.
, направленная вверх по наклонной плоскости (рис. 3.7, а). Найти ускорение и закон движения тела по плоскости.
Задача может быть решена как задача динамики материальной точки (п. 3.2). Это то же самое, что использовать дифференциальные уравнения поступательного движения тела (п. 3.7.1). Так как поступательное движение тела является прямолинейным, достаточно составить одно дифференциальное уравнение в проекции на направление движения – ось x (рис. 3.7, б). При составлении уравнения учитываются все внешние силы, действующие на тело: заданная сила 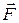 , сила тяжести тела
, сила тяжести тела 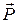 (по модулю
(по модулю  ), нормальная реакция плоскости
), нормальная реакция плоскости 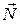 (
( 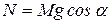 ), сила трения скольжения
), сила трения скольжения 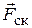 (
( 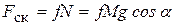 ).
).
Дифференциальное уравнение движения тела имеет вид: 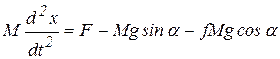 , откуда можно найти ускорение
, откуда можно найти ускорение 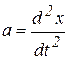 :
: 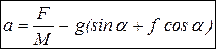 .Принимая во внимание, что ускорение
.Принимая во внимание, что ускорение 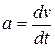 - производная по времени от скорости
- производная по времени от скорости 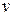 тела, и подставляя в полученное уравнение, после интегрирования с учетом начальных условий
тела, и подставляя в полученное уравнение, после интегрирования с учетом начальных условий 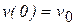 ,
, 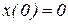 (начало отсчета оси x помещено в начальное положение
(начало отсчета оси x помещено в начальное положение 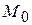 тела) можно найти скорость
тела) можно найти скорость 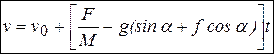 и закон движения тела по плоскости
и закон движения тела по плоскости 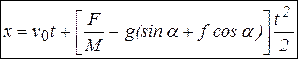 .
.
 Это же решение можно получить, используя теорему об изменении кинетической энергии материальной точки (п. 3.6.4). Изменение кинетической энергии на перемещении
Это же решение можно получить, используя теорему об изменении кинетической энергии материальной точки (п. 3.6.4). Изменение кинетической энергии на перемещении 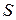 из начального положения
из начального положения 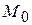 в конечное (произвольное, текущее) положение
в конечное (произвольное, текущее) положение 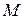 равно сумме работ сил, действующих на тело, на том же перемещении
равно сумме работ сил, действующих на тело, на том же перемещении 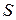 :
: 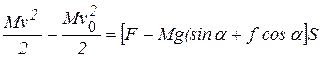 . Дифференцированием по времени уравнения кинетической энергии находится ускорение
. Дифференцированием по времени уравнения кинетической энергии находится ускорение 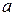 тела. Из этого же уравнения находится скорость
тела. Из этого же уравнения находится скорость 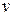 тела в функции перемещения
тела в функции перемещения 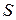 :
: 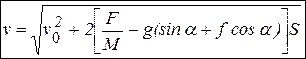 .
.
Дата добавления: 2014-12-01; просмотров: 2614;
