Динамика поступательного движения тела
При поступательном движении все точки тела движутся одинаково (ч. 2, п.2.3.1). Из теоремы об изменении количества движения или теоремы о движении центра масс механической системы (п. 3.4) получают дифференциальные уравнения поступательного движения тела:  ,
, 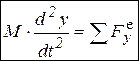 ,
, 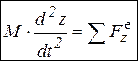 . Обозначения: x, y, z – координаты любой точки поступательно движущегося тела массой М (можно – центра масс С);
. Обозначения: x, y, z – координаты любой точки поступательно движущегося тела массой М (можно – центра масс С); 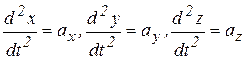 - проекции ускорения
- проекции ускорения 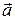 этой точки на оси; правые части уравнений, например,
этой точки на оси; правые части уравнений, например, 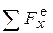 - сумма проекций всех внешних сил, действующих на тело, на соответствующую координатную ось.
- сумма проекций всех внешних сил, действующих на тело, на соответствующую координатную ось.
Эти уравнения во многом похожи на дифференциальные уравнения движения материальной точки (п. 3.2.1) и, значит, динамика поступательного движения тела сводится, по сути, к динамике одной любой его точки массой, равной массе М тела. При этом учитывают только внешние силы 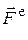 , действующие на тело.
, действующие на тело.
Дата добавления: 2014-12-01; просмотров: 901;
