Теорема об изменении кинетической энергии
Теорема об изменении кинетической энергии материальной точки. Изменение кинетической энергии материальной точки на некотором ее перемещении равно сумме работ сил, действующих на точку, на том же перемещении:  , где
, где 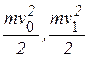 - кинетические энергии точки в начальном (скорость
- кинетические энергии точки в начальном (скорость 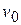 ) и конечном (скорость
) и конечном (скорость 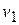 ) положениях.
) положениях.
Эта теорема дает возможность наиболее просто решать задачи динамики материальной точки, в которых устанавливается зависимость между действующими на точку силами, скоростью точки и пройденным точкой путем.
Теорема об изменении кинетической энергии механической системы. Изменение кинетической энергии механической системы на некотором ее перемещении равно сумме работ внешних и внутренних сил, действующих на систему, на том же перемещении:
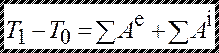 ,
,
где 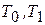 - кинетические энергии системы в начальном и конечном положениях.
- кинетические энергии системы в начальном и конечном положениях.
В отличие от других основных теорем динамики механической системы (п. 3.4, п. 3.5), эта теорема учитывает не только внешние, но и внутренние силы. Это связано с тем, что сумма работ внутренних сил механической системы в общем случае не равна нулю (в отличие от твердого тела, п. 3.6.3, случай 9).
Теоремой об изменении кинетической энергии механической системы удобно пользоваться при исследовании динамики твердых тел или системы твердых тел. Тогда сумма работ внутренних сил системы на любом перемещении равна нулю, и можно пользоваться уравнением 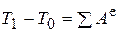 .
.
С помощью этой теоремы можно находить действующие на систему силы, линейные и угловые перемещения тел, входящих в систему, линейные и угловые скорости этих тел. Дифференцируя по времени уравнение  , составленное для произвольного перемещения системы, можно также находить ускорения отдельных точек или тел системы. Фактически это означает использование теоремы об изменении кинетической энергии механической системы в дифференциальной форме:
, составленное для произвольного перемещения системы, можно также находить ускорения отдельных точек или тел системы. Фактически это означает использование теоремы об изменении кинетической энергии механической системы в дифференциальной форме: 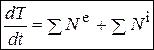 . Здесь
. Здесь  - сумма мощностей всех внешних и внутренних сил механической системы.
- сумма мощностей всех внешних и внутренних сил механической системы.
По определению, мощность N силы 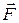 - это скалярная величина, характеризующая быстроту совершения работы этой силой (скорость работы силы) и равная отношению элементарной работы dA к бесконечно малому промежутку времени dt, за который она совершена:
- это скалярная величина, характеризующая быстроту совершения работы этой силой (скорость работы силы) и равная отношению элементарной работы dA к бесконечно малому промежутку времени dt, за который она совершена: 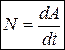 . С учетом разных способов определения работы (табл. 3.3) мощность силы
. С учетом разных способов определения работы (табл. 3.3) мощность силы 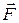 также может определяться по-разному:
также может определяться по-разному: 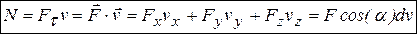 , где
, где 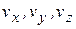 - проекции скорости
- проекции скорости  точки приложения силы
точки приложения силы 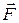 .
.
Дата добавления: 2014-12-01; просмотров: 2485;
