Кинетическая энергия

Наряду с количеством движения (п. 3.4) и моментом количества движения (п. 3.5) в механике используется еще одна, но не векторная, а скалярная динамическая характеристика движения – кинетическая энергия. Кинетическая энергия материальной точки Т находится как половина произведения массы m материальной точки на квадрат 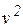ее скорости: .

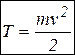Кинетическая энергия механической системы – это сумма кинетических энергий всех материальных точек системы: .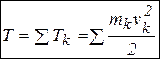

Для вычисления кнетической энергии механической системы удобно пользоваться теоремой Кёнига. Кинетическая энергия механической системы равна сумме кинетической энергии центра масс системы, масса которого равна массе всей системы, и кинетической энергии системы в ее относительном движении по отношению к центру масс: 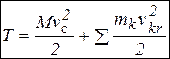; здесь M – масса системы, 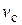- скорость центра масс, 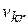- относительная скорость k-й точки системы относительно центра масс.

В частных случаях, когда механическая система представляет собой твердое тело массой М, кинетическая энергия находится так:

Поступательное движение - 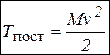, 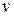- скорость любой точки тела;

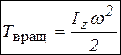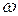Вращательное движение - , - момент инерции тела относительно оси вращения z, - угловая скорость вращения тела;

Плоскопараллельное движение - 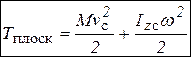, 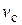- скорость центра масс, 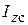- момент инерции тела относительно оси z, проходящей через центр масс С.