Потенциальная энергия

Силы называются потенциальными, если работа этих сил зависит только от начального и конечного положений точки приложения силы, и не зависит от траектории. Иначе – работа потенциальной силы 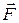вдоль любой произвольной замкнутой траектории точки приложения силы равна нулю: 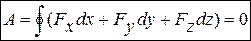. Для выполнения этого условия необходимо и достаточно, чтобы подынтегральное выражение (элементарная работа силы 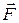) было полным дифференциалом некоторой скалярной функции координат 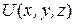, которая называется силовой функцией: 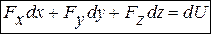. Потенциальная сила 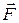связана с силовой функцией 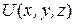зависимостью .

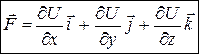Если потенциальные силы и силовая функция зависят только от координат x, y, z и не зависят от времени t ( 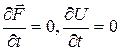), силы называются стационарными. Работа А стационарной потенциальной силы 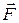при перемещении точки ее приложения из начального М₀ в конечное М₁ положение равна разности значений силовой функции в конечной и начальной точках: .

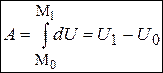Силы, работа которых зависит от траектории точки приложения силы, называются непотенциальными. Примерами потенциальных сил являются силы тяжести, силы упругости (п. 3.6.3, случаи 2, 3), непотенциальные силы – например, сила трения скольжения (п. З.6.3, случай 4).

Вместо выражения «потенциальные силы» часто говорят «потенциальные поля», понимая под потенциальным полем область пространства, в точках которого действуют потенциальные силы. Например, вблизи поверхности Земли действуют потенциальные силы тяжести, иначе – потенциальное поле сил тяжести.

Работа сил потенциального поля на перемещении точки из конечного М₁ положения в начальное М₀ называется потенциальной энергией точки. В общем случае потенциальная энергия 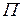– функция координат x, y, z точки, то есть 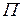= 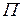(x,y,z). Точно также определяют потенциальную энергию механической системы – как сумму работ сил потенциального поля, приложенных к точкам механической системы.

Работа потенциальных сил, приложенных к точкам механической системы, на любом перемещении равна разности значений потенциальной энергии в начальном (0) и конечном (1) положениях системы: 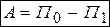. Таким образом, потенциальная энергия 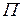отличается от силовой функции U знаком минус.