Структура матриц, используемых в методе КЭ

Пусть используется конечный элемент, содержащий n узлов. В этом случае вектор узловых перемещений элемента, вектор узловых сил элемента, матрица жесткости элемента оказываются логически разделенными на блоки, а именно:

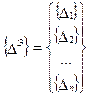, (7.20)

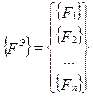, (7.21)

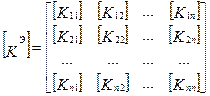, (7.22)

где

· блоки 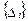содержат узловые перемещения, относящиеся к i-му узлу,

· блоки 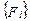содержат узловые силы, относящиеся к i-му узлу,

· блоки 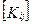содержат коэффициенты жесткости, связывающие силы, относящиеся к i-му узлу, с перемещениями j-го узла, которые можно трактовать как реакции, возникающие в закрепленных степенях свободы i-го узла в результате смещения j-й узловой точки.

Стоит помнить, что матрица жесткости симметрична и поэтому

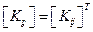. (7.23)

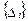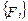Наполнение векторов и , относящихся к отдельной узловой точки зависит от характера решаемой задачи.

Так при решении задачи определения напряженного состояния тонкой пластины нагруженной в своей плоскости (плоской задачи теории упругости) указанные вектора могут иметь следующую структуру:

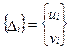, (7.24)

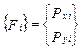, (7.25)

где 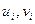смещения i-го узла по осям x и y, а компоненты 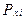и 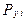- узловые силы приложенные в этом узле (рис 7.2).

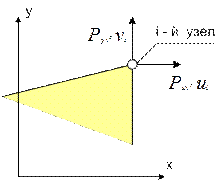
Рис. 7.2

При решении задачи изгиба пластины наполнение указанных векторов будет совсем другим (рис. 7.3):

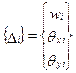, (7.26)

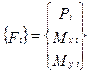, (7.27)

где 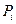- узловая сила, приложенная по нормали к поверхности плиты (вдоль оси z); 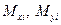- пары сил, приложенных в i-м узле соответственно в плоскостях xz и yz;

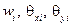- прогиб и угловые перемещения (повороты) i-го узла в тех же направлениях.

Имея величины перемещений в узлах, перемещения во внутренних точках элемента можно выразить путем интерполяции с помощью набора алгебраических функций 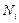, которые известны как функции формы. Это делается с помощью формулы 7.5 следующим образом:

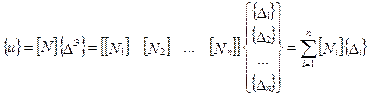, (7.28)

где n – число узловых точек конечного элемента, причем блоки 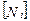имеют диагональную структуру и могут быть построены по правилу

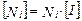, (7.29)

где 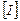- единичная матрица размером 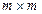, а 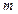- число степеней свободы в узле.

В качестве примера приведем структуру матрицы функций формы для трехузлового конечного элемента с двумя степенями свободы в узле:

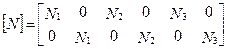(7.30)

Матрица деформаций 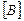в соответствии с формулой (7.9) формируется путем умножения матричного оператора 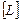на матрицу функций формы 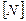. По этой причине матрица 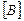как и матрица функций формы 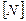будет иметь блочную структуру:

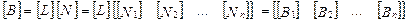(7.31)

и тогда соотношение (7.8) для элемента, содержащего n узлов, может быть развернуто следующим образом:

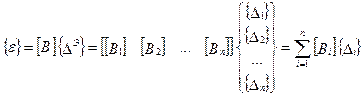(7.32)