Сборка глобальной системы уравнений МКЭ
Для разъяснения процедуры сборки глобальной матрицы жесткости и глобального вектора узловых сил рассмотрим для начала простой пример стержня, загруженного осевой нагрузкой представленного двумя квадратичными конечными элементами типа 1D3. Каждый i-й узел такого конечного элемента будет иметь одну степень свободы.

Рис. 7.3
Предположим, что для каждого из трех элементов вычислена матрица жесткости и вектор узловых сил. Таким образом, мы имеем в распоряжении следующие матрицы:
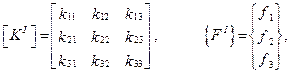 (7.33)
(7.33)
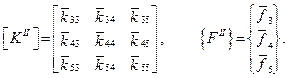
Потенциальная энергия может быть вычислена отдельно для каждого элемента:
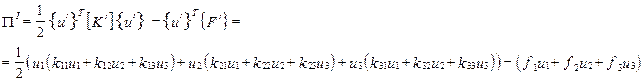
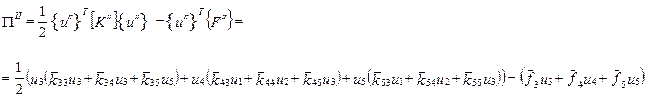
Общая потенциальная энергия равняется сумме потенциальных энергий элементов:
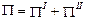 (7.34)
(7.34)
Теперь применим теорему о минимуме потенциальной энергии системы.
Приравнивая к нулю первые производные от потенциальной энергии по каждому из узловых перемещений, получим:
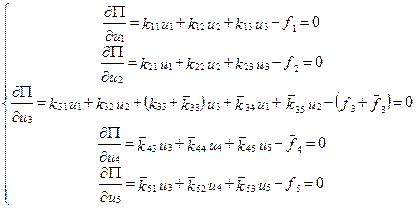
Сформированная система уравнений может быть записана в матричной форме
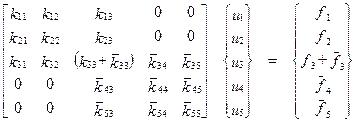 . (7.35)
. (7.35)
Видно, что коэффициенты жесткости, относящиеся к 3-му узлу и входящие в матрицы жесткости как первого, так и второго элементов, при сборке матрицы жесткости всей конструкции суммируются
Несколько более сложный характер будет иметь процесс сборки для двумерных и трехмерных сеток конечных элементов. Продемонстрируем порядок формирования глобальных матриц на примере плоской сетки состоящей их трех квадратичных конечных элементов типа 2D8 (Рис. 7.4). На приведенном рисунке показана общая (глобальная) нумерация узловых точек сетки.
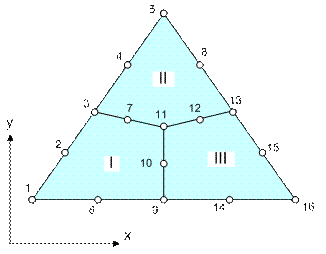
Рис. 7.4
Для начала рассмотрим первый конечный элемент (рис. 7.5). В кружочках приведены глобальные номера узлов сетки, а внутри конечного элемента указана против часовой стрелки их локальная нумерация от 1 до 8, начиная с правого верхнего узла.
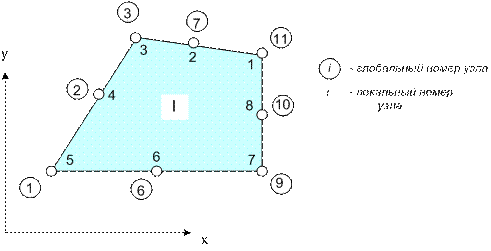
Рис. 7.5
Матрица жесткости данного элемента может быть представлена в блочном виде (рис. 7. 6), на котором каждый квадратный блок 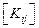 имеет размерность
имеет размерность 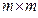 , где m-число степеней свободы в узле, и содержит, как указывалось выше, реакции возникающие в
, где m-число степеней свободы в узле, и содержит, как указывалось выше, реакции возникающие в 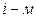 закрепленном в результате смещений
закрепленном в результате смещений 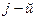 узловой точки. Блоки матрицы жесткости элемента упорядочены в соответствии с локальной нумерацией узлов, но указаны также и их глобальные номера. Поскольку матрица жесткости обладает свойством симметрии, отсутствует необходимость в хранении ее нижней треугольной части. На этом же рисунке показан и вектор узловых сил данного конечного элемента.
узловой точки. Блоки матрицы жесткости элемента упорядочены в соответствии с локальной нумерацией узлов, но указаны также и их глобальные номера. Поскольку матрица жесткости обладает свойством симметрии, отсутствует необходимость в хранении ее нижней треугольной части. На этом же рисунке показан и вектор узловых сил данного конечного элемента.
При включении коэффициентов жесткости и узловых сил, относящихся к данному конечному элементу, в соответствующие глобальные матрицы, необходимо учитывать несоответствие глобальной и локальной нумерации узлов элемента. Так, например, блок 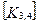 в глобальной матрице жесткости (рис. 7.7) должен стоять на пересечении 3-й строки и 2-го столбца и, в силу симметрии, на пересечении 2-й строки и 3-го столбца поскольку 4-му узлу данного конечного элемента соответствует глобальный номер 2.
в глобальной матрице жесткости (рис. 7.7) должен стоять на пересечении 3-й строки и 2-го столбца и, в силу симметрии, на пересечении 2-й строки и 3-го столбца поскольку 4-му узлу данного конечного элемента соответствует глобальный номер 2.
При включении в глобальные матрицы жесткостей и узловых сил для всех последующих конечных элементов, соответствующие жесткости и узловые силы должны суммироваться с теми, которые уже были размещены там ранее.
| глобальные → | 11 | 7 | 3 | 2 | 1 | 6 | 9 | 10 | ||||
| локальные → | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||||
| 11 | 1 | 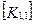
| 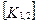
| 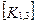
| 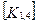
| 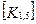
| 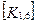
| 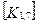
| 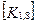
| 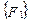
| ||
| 7 | 2 | 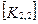
| 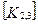
| 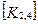
| 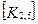
| 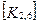
| 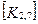
| 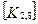
| 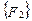
| |||
| 3 | 3 | 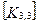
| 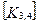
| 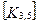
| 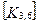
| 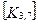
| 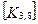
| 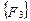
| ||||
| 2 | 4 | 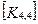
| 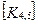
| 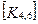
| 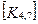
| 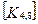
| 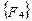
| |||||
| 1 | 5 | 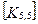
| 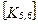
| 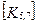
| 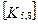
| 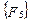
| ||||||
| 6 | 6 | 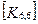
| 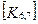
| 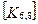
| 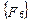
| |||||||
| 9 | 7 | симметрично | 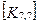
| 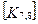
| 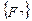
| |||||||
| 10 | 8 | 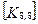
| 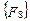
| |||||||||
| ↑ глоб. | ↑ лок. | матрица жесткости для I элемента | вектор узловых сил |
Рис. 7.6
Описанный алгоритм называется сборкой глобальной системы уравнений метода конечных элементов.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | → | |
| 1 | 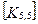
| 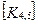
| 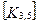
| 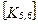
| 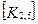
| 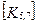
| 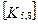
| 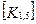
| |||||
| 2 | 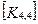
| 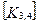
| 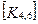
| 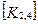
| 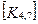
| 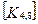
| 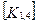
| ||||||
| 3 | 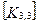
| 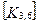
| 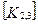
| 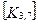
| 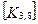
| 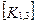
| |||||||
| 4 | |||||||||||||
| 5 | |||||||||||||
| 6 | 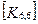
| 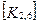
| 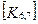
| 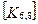
| 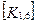
| ||||||||
| 7 | 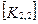
| 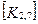
| 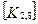
| 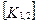
| |||||||||
| 8 | |||||||||||||
| 9 | 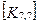
| 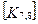
| 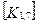
| ||||||||||
| 10 | 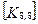
| 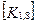
| |||||||||||
| 11 | 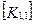
| ||||||||||||
| ↓ |
Рис. 7.7
Дата добавления: 2015-01-02; просмотров: 1830;
