Нагрузки и воздействия

В МКЭ все действующие на тело нагрузки, к которым относятся

· сосредоточенные силы,

· силы, распределенные по поверхности,

· распределенные по объему гравитационные силы

приводятся к эквивалентным системам сил, приложенным в узловых точках.

Покажем как сосредоточенную силу, приложенную в произвольной точке, привести к эквивалентной системе узловых сил.

Рассмотрим случай (рис. 7.8), когда сосредоточенная сила приложена в произвольной точке на одной из сторон плоского квадратичного изопараметрического элемента.

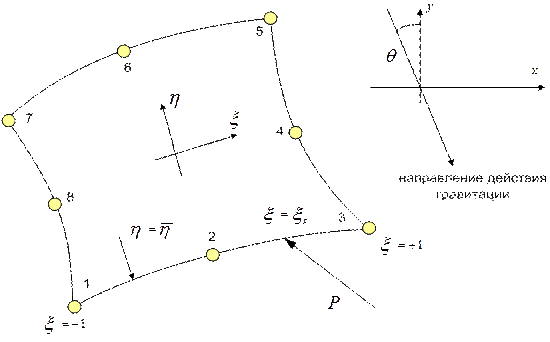
Рис.7.8

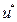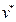Дадим виртуальные смещения и соответственно по осям x и y, узлам, расположенным на рассматриваемой стороне элемента. Тогда для i-го узла можно написать равенства

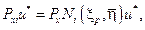(7.36)

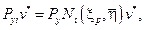
где 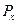и 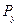компоненты силы Р; 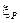― локальная координата точки приложения силы, а 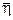― постоянное значение другой локальной координаты, определяющее положение рассматриваемой стороны (+1 или -1).

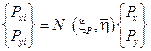. (7.37)

Таким же образом с помощью функций формы глобальные координаты точки, в которой приложена сосредоточенная сила, могут быть выражены через координаты узлов:

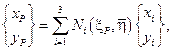(7.38)

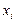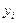где и - координаты i-го узла рассматриваемой стороны.

Гравитационная сила действует на каждый элементарный объем тела и ее направление в общем случае может не совпадать с направлением координатных осей x и y. Ее величина равняется

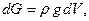
где 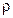― удельная плотность материала конструкции, 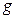― ускорение свободного падения.

Компоненты этой силы по осям х и у соответственно равны:

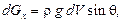
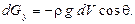
Дадим виртуальные смещения 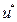и 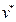в направлении осей х и у. В соответствии с принципом виртуальных работ получим следующие выражения:

,

,

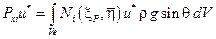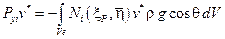где 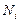― функции формы, а индекс i для рассматриваемого типа конечного элемента изменяется от 1 до 8.

Отсюда следует матричное выражение для эквивалентных узловых сил

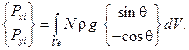
Численное интегрирование может быть выполнено по правилу Гаусса:

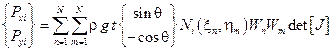
где t ― толщина элемента; 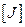― матрица Якоби; 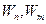- весовые множители.

На каждую из сторон конечного элемента в том случае, когда она выходит на поверхность тела, могут действовать распределенные нормальные и касательные внешние силы (рис.7.9). Применение квадратичных конечных элементов позволяет учитывать распределенные воздействия, которые изменяются по квадратичному закону, используя приведение их к сосредоточенным силам, приложенным в узлах КЭ.

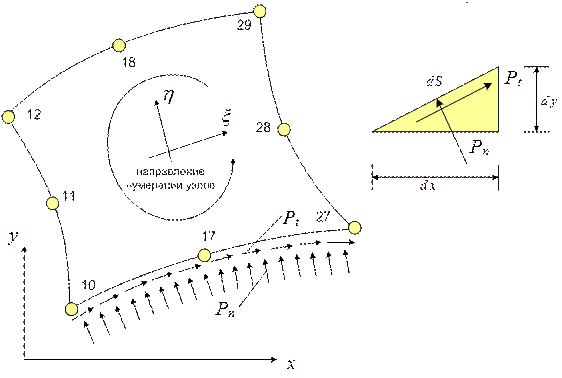
Рис.7.9

Список рекомендуемой литературы:

1. Норри Д., де Фриз Ж. Введение в метод конечных элементов. М.: Мир. 1981.

2. Постнов В.А. Численные методы расчета судовых конструкций. «Судостроение» Ленинград. 1977.

3. Галлагер Р. Метод конечных элементов. Основы: Пер. с англ. — М.: Мир, 1984

4. Деклу Ж. Метод конечных элементов: Пер. с франц. — М.: Мир, 1976

5. Зенкевич О. Метод конечных элементов в технике — М.: Мир, 1975.

6. Зенкевич О., Морган К. Конечные элементы и аппроксимация: Пер. с англ. — М.: Мир, 1986

7. Сегерлинд Л. Применение метода конечных элементов – М.: Мир, 1979. – 392 С.

8. Turner M.J., Clouhg R. W., Martin H.C., Topp L.J. Stiffness and Deflection Analysis of Complex Structures // J. Aeronaut. Sci. – 1956. – №23. – P.805-824

9. Дж. Голуб, Ч.Ван Лоун Матричные вычисления. — М.: Мир, 1999.

10. Беллман Р. Введение в теорию матриц. — М.: Мир, 1969.

11. Гантмахер Ф. Р. Теория матриц (2-е издание). — М.: Наука, 1966.

12. Ланкастер П. Теория матриц. — М.: Наука, 1973.

13. http://www.cneat.ru/lex2.html

14. Melosh R.J. Basis for Derivation of Matrices for the Direct Stiffness method. // J. Am. Inst. For Aeronautics and Astronautics. – 1965. - №1. – P.1631-1637

15. Капустин С.А. Метод конечных элементов в задачах механики деформируемых тел//Н. Новгород, Изд-во Нижегород. ун-та, 2002, 180 с.

16. Работнов Ю.Н. Механика деформируемого твердого тела. М.: Наука, 1988, 712 с.

17. Кашеварова, Г.Г. Основы автоматизации проектирования в строительстве: курс лекций / Г.Г. Кашеварова. - Пермь: Ивд-во Перм. гос. техн. ун-та, 2007.-300 с.