Матричная запись соотношений Коши и закона Гука
При матричной формулировке уравнений теории упругости принято информацию о смещениях точек тела, а также о деформированном и напряженном состоянии, учитывая симметрию соответствующих тензоров, представлять векторами:
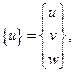
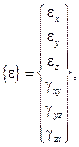
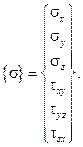 (6.6-6.8)
(6.6-6.8)
В этом случае, введя матричный дифференциальный оператор 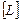 , соотношения Коши можно записать в матричной форме следующим образом:
, соотношения Коши можно записать в матричной форме следующим образом:
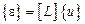 , (6.9)
, (6.9)
где 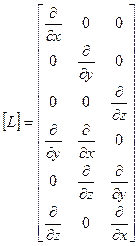 . (6.10)
. (6.10)
Закон Гука нетрудно записать как в прямой, так и в обратной форме:
 (6.11-6.12)
(6.11-6.12)
где матрица упругих постоянных 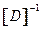 , как это видно из соотношений (6.5), имеет следующие постоянные компоненты:
, как это видно из соотношений (6.5), имеет следующие постоянные компоненты:
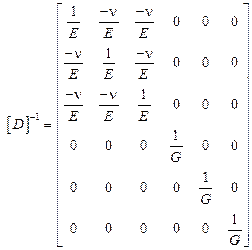 , (6.13)
, (6.13)
где 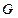 - модуль упругости при сдвиге (модуль сдвига), который равен
- модуль упругости при сдвиге (модуль сдвига), который равен
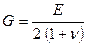 (6.14)
(6.14)
Путем обращения приведенной выше матрицы, получается матрица перехода от деформаций к напряжениям:
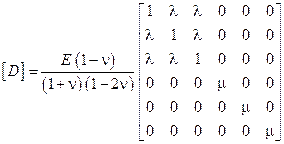 , (6.15)
, (6.15)
где 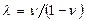 ,
, 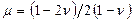 .
.
Дата добавления: 2015-01-02; просмотров: 2912;
