Дискретизация задачи. Минимум потенциальной энергии системы

В реальной конструкции число степеней свободы ее внутренних точек бесконечно, и поэтому замкнутое решение задачи зачастую становится невозможным. При численной постановке задачи приближенное решение строится с использованием конечного числа степеней свободы.

Как указывалось выше, в методе конечных элементов среда разделяется на серию элементов, которые взаимодействуют в конечном числе узловых точек. Этот процесс называется дискретизацией задачи.

В задачах анализа конструкций окончательные уравнения МКЭ могут быть получены минимизацией общей потенциальной энергии системы.

Потенциальная энергия конструкции П является суммой энергии деформации U и потенциала внешних сил V, то есть:

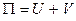(7.1)

Сформулируем принцип минимума потенциальной энергии, как это делается в строительной механике:

Чтобы считаться допустимыми, перемещения

· должны быть непрерывными,

· должны удовлетворять условиям закрепления.

Так на рис. 7.1 приведены примеры допустимых и недопустимых перемещений.

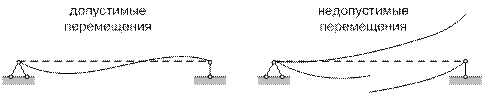
Рис. 7.1

Пользуясь матричными обозначениями, выразим энергию деформаций:

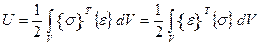, (7.2)

где 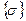- вектор, содержащий компоненты напряжений или усилий,

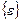- вектор, содержащий компоненты деформаций.

Потенциал нагрузок, приложенных в объеме конструкции и на ее поверхности равен:

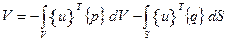(7.3)

где 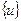- вектор перемещений внутренних точек конструкции,

- вектор сил, распределенных по объему материала,

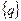- вектор сил, распределенных по поверхности тела.

Выразим величину потенциальной энергии, запасенной телом при деформировании:

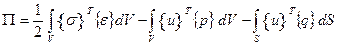(7.4)

В МКЭ перемещения произвольных точек внутри конечного элемента выражаются через узловые перемещения с помощью матриц функций формы:

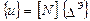, (7.5)

где 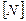- матрица функций формы, 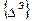- вектор узловых перемещений конечного элемента.

Функции формы формируются по аналогии с координатными функциями, которые используются в вариационных методах, и должны удовлетворять условиям полноты, линейной независимости и принадлежать энергетическому пространству, связанному с исходным дифференциальным оператором.

Необходимо отметить, что в МКЭ эти требования формируются несколько другой форме. Так, одним из свойств функции формы является ее равенство нулю во всех узлах, кроме одного.

Деформации в точках внутри конечного элемента получаются путем дифференцирования перемещения точек тела с помощью матричного дифференциального оператора 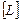подобно тому, как это делается, например, в теории упругости при записи соотношений Коши:

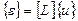(7.6)

Подставляя в (7.6) соотношение (7.5), получаем выражение вектора деформаций через перемещения узловых точек конечного элемента

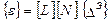(7.7)

или

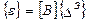, (7.8)

где

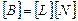(7.9)

матрица, не совсем удачно называемая матрицей деформаций, которая обычно строится с использованием производных от функций формы конечного элемента.

Напряжения выражаются через деформации с помощью закона Гука

, (7.10)

или с учетом (7.8):

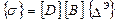, (7.11)

где 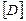- матрица упругих постоянных материала конструкции.

Таким образом, все неизвестные функции, определяющие напряженно-деформированное состояние внутри конечного элемента оказались выраженными через перемещения узловых точек.

Подставляя в (7.4) выражения (7.5), (7.8) и (7.11) и вычисляя интегралы по объему или по поверхности только одного конечного элемента, получим развернутое выражение потенциальной энергии, запасенной в теле данного конечного элемента:

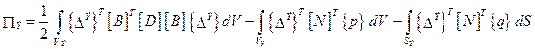, (7.12)

где 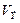- объем конечного элемента,

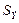- загруженная поверхность конечного элемента.

Возьмем первые производные от полученной потенциальной энергии по узловым перемещениям. Естественно, что их число будет равно числу степеней свободы элемента и, следовательно, их можно представить в виде вектора:

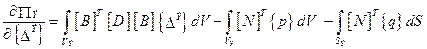(7.13)

или, учитывая то, что перемещения узлов не зависят от пространственных координат x, y, z и, следовательно, могут быть вынесены из под знака интеграла

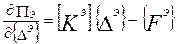, (7.14)

где

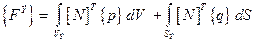- (7.15)

вектор эквивалентных узловых сил, к которому приводятся все поверхностные и распределенные по объему силы, действующие на данный конечный элемент, а

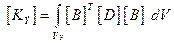- (7.16)

матрица жесткости конечного элемента.

Представим, что модель содержит всего один конечный элемент. В этом случае для экстремальности потенциальной энергии необходимо обращение в ноль первых производных по всем узловым степеням свобода, то есть

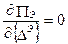, (7.17)

что приводит к системе линейных алгебраических уравнений вида

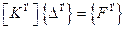. (7.18)

Когда конструкция моделируется набором конечных элементов, потенциальная энергия всей конструкции будет складываться из потенциальных энергий отдельных конечных элементов, то есть

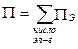(7.19)

В силу этого глобальная система уравнений метода конечных элементов может быть получена суммированием по всем конечным элементам выражений, полученных по формуле (7.19) с последующим приведением подобных членов (суммированием коэффициентов жесткости, относящихся к разным конечным элементам, но к одному и тому же узловому перемещению) и приравниванием полученных выражений к нулю. Эта процедура называется сборкой системы уравнений метода конечных элементов.

Таким образом, общая процедура метода включает в себя ряд последовательных этапов:

· разбивку тела конструкции на конечные элементы;

· вычисление матрицы жесткости и вектора узловых сил для каждого конечного элемента;

· сборку жесткостей и узловых сил отдельных конечных элементов в глобальную матрицу жесткости и глобальный вектор узловых сил;

· решение системы линейных алгебраических уравнений и нахождение узловых перемещений;

· вычисление величин, характеризующих напряженное состояние, во внутренних точках конечного элемента.

Каждый этап решения задачи при программировании оформляется в виде отдельной процедуры.