Развитие математики в XVIII в.
XVIII век характеризуется решительной победой капиталистического способа производства. Решение научно-технических задач становится делом общегосударственной важности, и математика в этот период стала необходимой для развития промышленности, военной техники, кораблестроения, составления географических карт.
Математики XVIII века работали одновременно в области естествознания и техники. Труд Лагранжа, появившийся через сто лет после работ Ньютона, показал, как много результатов можно получить в механике благодаря мощным методам математического анализа. Лагранж создал основы аналитической механики. Монументальное произведение Лапласа “Небесная механика” подвело итоги всех предшествующих работ в этой области.
Особое место занимают многочисленные работы, сделанные академиками Петербургской Академии наук. Здесь, кроме работ по математическому анализу, преобладающее значение получили исследования, связанные с его приложениями к проблемам механики, астрономии, физики, техники. Именно это направление ярко выражено в трудах Даниила Бернулли, который был в первой группе приглашенных из-за границы ученых.
Петербург, как магнит, притягивал многих западноевропейских ученых, особенно из Германии и Швейцарии. Блестящие перспективы работы в России побудили к переезду в Петербург Николая и Даниила Бернулли (сыновей профессора математики в Базельском университете Иоганна Бернулли). Заметим, что семья Бернулли (в трех поколениях) сыграла большую роль в развитии математических наук с конца XVII до XVIII столетия.
Круг интересов Д.Бернулли включал проблемы дифференциальных уравнений, физики, механики, гидродинамики, теории вероятностей и статистики.
Остановимся на творчестве младшего по возрасту члена академической группы математиков - великого Леонарда Эйлера.
Воспитанник Базельского университета Леонард Эйлер в 1727 г. (и до самой кончины в 1783 г.) связал свою судьбу с русской Академией наук. По приезде в Петербург он занял место профессора и включился в активную научную, педагогическую и научно-организаторскую деятельность. Эйлер получил значительные результаты в механике, занимался кораблестроением и оптикой. Эйлер ввел в математику символ f(x) для функции и показал, что функциональная зависимость является основным объектом изучения математического анализа. В математическом творчестве Эйлера на первом месте стоит анализ бесконечно малых, затем - теория чисел, геометрия, алгебра и комбинаторика, теория вероятностей. Он явился основателем нескольких больших дисциплин: вариационного исчисления, учения об элементарных функциях комплексного переменного, теории дифференциальных уравнений, учения о специальных функциях, учения о тригонометрических рядах.
Огромно наследие Эйлера. Список его трудов насчитывает более 850 названий. Из 72 томов его сочинений 29 относится к “чистой” математике, 31 том - к механике и астрономии, 12 - к физике и разным вопросам.
Эйлер оказал огромное влияние на все развитие математических наук. Особое значение имело творчество Эйлера для науки в России.
К этому же периоду относятся и другие разработки в математике: были введены и изучены функции нескольких переменных, обобщалась теория дифференцирования и интегрирования функций многих переменных, способы вычисления частных производных, кратных и криволинейных интегралов. Основным инструментом в изучении функций стал аппарат их разложения в бесконечные степенные ряды. В XVIII веке были найдены степенные ряды для всех элементарных функций.
Уже Ньютон и Лейбниц видели в бесконечных рядах не только средство приближенных вычислений, но своего рода универсальный ключ к задачам анализа, которые не удается решить в конечной форме. Ряды оказались полезными для вычисления корней уравнений, не разрешающихся в радикалах, для представления неэлементарных интегралов, интегрирования дифференциальных уравнений и т.д. Эйлер необычайно умножил приложения бесконечных рядов, впервые приступил с их помощью к исследованию функций.
В XVIII веке понятие сходимости рядов не было еще точно установлено. Математики часто оперировали расходящимися рядами, приписывая им определенные суммы. Это заблуждение приводило к неразрешимым противоречиям.
Вот пример такого ряда. В 1710 г. итальянец Гранди доказывал существование сверхъестественной силы при помощи известного ряда:
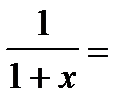 1 - х + х2 - х3 + х4 - х5 + ¼ . (1)
1 - х + х2 - х3 + х4 - х5 + ¼ . (1)
Полагая в этом равенстве х=1, он получил
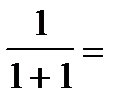 1 - 1 + 1 - 1 + 1 - 1 + ¼ . (2)
1 - 1 + 1 - 1 + 1 - 1 + ¼ . (2)
Группируя попарно слагаемые в правой части, пришел к равенству:
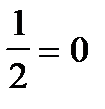 .
.
Гранди объяснил этот результат как символ “создания мира из ничего”. Поэтому и знаменитый норвежский математик Г. Абель (1802–1829), приступая к исследованию рядов, называл расходящиеся ряды “дьявольским измышлением”.
В наше время каждый студент знает, что равенство (1) справедливо лишь при |х| < 1, а при х=1 получается расходящийся ряд, который не имеет никакой суммы.
Кроме Эйлера разработкой теории рядов занимались Абель, французы Коши (1789-1859), Даламбер (1717-1783), немецкие ученые Лейбниц, Дирихле, Риман. Эта работа велась на протяжении полутора столетий, продолжается она и до сих пор.
В XVIII веке из математического анализа выделился ряд важных математических дисциплин: теория дифференциальных уравнений, вариационное исчисление, теория функций комплексного переменного. Из геометрических приложений анализа выделилась дифференциальная геометрия. В XVIII веке началась разработка теории вероятностей.
В XVIII веке математики использовали много различных способов изложения анализа, но ни один из них не мог удовлетворительно объяснить его основы. Только теория пределов справилась с этой задачей. Сторонники теории пределов - Даламбер, Абель, Коши, русский математик Гурьев С.Е. (1764-1813) - неустанно ее совершенствовали. Работа по созданию теории пределов продолжена уже в XIX веке немецким математиком Вейерштрассом (70-е годы).
Последующая разработка теории пределов потребовала построения теории действительного числа. Почти одновременно в 1872 г. были построены такие теории Кантором, Вейерштрассом и Дедекиндом. Различные по форме, эти теории главным образом решали одну проблему - существование непрерывности числовой прямой.
Изучение действительных чисел привело, в свою очередь, к рассмотрению бесконечных множеств.
Дата добавления: 2014-12-30; просмотров: 3923;
